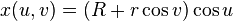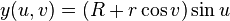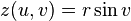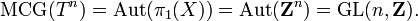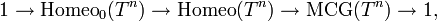In geometry, a torus (pl. tori) is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle. In most contexts it is assumed that the axis does not touch the circle – in this case the surface has a ring shape and is called a ring torus or simply torus if the ring shape is implicit.
Other types of torus include the horn torus, which is generated when the axis is tangent to the circle, and the spindle torus, which is generated when the axis is a chord of the circle. A degenerate case is when the axis is a diameter of the circle, which simply generates the surface of a sphere. The ring torus bounds a solid known as a toroid. The adjective toroidal can be applied to tori, toroids or, more generally, any ring shape as in toroidal inductors and transformers. Real world examples of (approximately) toroidal objects include doughnuts, inner tubes, many lifebuoys, O-rings and vortex rings.
In topology, a ring torus is homeomorphic to the Cartesian product of two circles: S1 × S1, and the latter is taken to be the definition in that context. It is a compact 2-manifold of genus 1. The ring torus is one way to embed this space into Euclidean space, but another way to do this is the Cartesian product of the embedding of S1 in the plane. This produces a geometric object called the Clifford torus, surface in 4-space.
The word torus comes from the Latin word meaning cushion.[1]
Contents |
Geometry
A torus can be defined parametrically by:[2]
where
- u,v are in the interval [0, 2π),
- R (or A) is the distance from the center of the tube to the center of the torus,
- r (or a) is the radius of the tube.
R and r are also known as the “major radius” and “minor radius”, respectively. The ratio of the two is known as the “aspect ratio“. A doughnut has an aspect ratio of 2 to 3.
An implicit equation in Cartesian coordinates for a torus radially symmetric about the z-axis is
or the solution of f(x,y,z) = 0, where
Algebraically eliminating the square root gives a quartic equation,
The three different classes of standard tori correspond to the three possible relative sizes of r and R. When R > r, the surface will be the familiar ring torus. The case R = r corresponds to the horn torus, which in effect is a torus with no “hole”. The case R < r describes the self-intersecting spindle torus. When R = 0, the torus degenerates to the sphere.
The surface area and interior volume of this torus are easily computed using Pappus’s centroid theorem giving[3]
These formulas are the same as for a cylinder of length 2πR and radius r, created by cutting the tube and unrolling it by straightening out the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.
As a torus is the product of two circles, a modified version of the spherical coordinate system is sometimes used. In traditional spherical coordinates there are three measures, R, the distance from the center of the coordinate system, and θ and φ, angles measured from the center point. As a torus has, effectively, two center points, the centerpoints of the angles are moved; φ measures the same angle as it does in the spherical system, but is known as the “toroidal” direction. The center point of θ is moved to the center of r, and is known as the “poloidal” direction. These terms were first used in a discussion of the Earth’s magnetic field, where “poloidal” was used to denote “the direction toward the poles”.[4] In modern use these terms are more commonly used to discuss magnetic confinement fusion devices.
Topology
Topologically, a torus is a closed surface defined as the product of two circles: S1 × S1. This can be viewed as lying in C2 and is a subset of the 3-sphere S3 of radius √2. This topological torus is also often called the Clifford torus. In fact, S3 is filled out by a family of nested tori in this manner (with two degenerate circles), a fact which is important in the study of S3 as a fiber bundle over S2 (the Hopf bundle).
The surface described above, given the relative topology from R3, is homeomorphic to a topological torus as long as it does not intersect its own axis. A particular homeomorphism is given by stereographically projecting the topological torus into R3 from the north pole of S3.
The torus can also be described as a quotient of the Cartesian plane under the identifications
- (x,y) ~ (x+1,y) ~ (x,y+1).
Or, equivalently, as the quotient of the unit square by pasting the opposite edges together, described as a fundamental polygon ABA − 1B − 1.
The fundamental group of the torus is just the direct product of the fundamental group of the circle with itself:
Intuitively speaking, this means that a closed path that circles the torus’ “hole” (say, a circle that traces out a particular latitude) and then circles the torus’ “body” (say, a circle that traces out a particular longitude) can be deformed to a path that circles the body and then the hole. So, strictly ‘latitudinal’ and strictly ‘longitudinal’ paths commute. This might be imagined as two shoelaces passing through each other, then unwinding, then rewinding.
If a torus is punctured and turned inside out then another torus results, with lines of latitude and longitude interchanged.
The first homology group of the torus is isomorphic to the fundamental group (this follows from Hurewicz theorem since the fundamental group is abelian).
Two-sheeted cover
The 2-torus double-covers the 2-sphere, with four ramification points. Every conformal structure on the 2-torus can be represented as a two-sheeted cover of the 2-sphere. The points on the torus corresponding to the ramification points are the Weierstrass points. In fact, the conformal type of the torus is determined by the cross-ratio of the four points.
n-dimensional torus
The torus has a generalization to higher dimensions, the n–dimensional torus, often called the n–torus for short. (This is one of two different meanings of the term “n-torus”.) Recalling that the torus is the product space of two circles, the n-dimensional torus is the product of n circles. That is:
The torus discussed above is the 2-dimensional torus. The 1-dimensional torus is just the circle. Just as for the 2-torus, the n-torus can be described as a quotient of Rn under integral shifts in any coordinate. That is, the n-torus is Rn modulo the action of the integer lattice Zn (with the action being taken as vector addition). Equivalently, the n-torus is obtained from the n-dimensional hypercube by gluing the opposite faces together.
An n-torus in this sense is an example of an n-dimensional compact manifold. It is also an example of a compact abelian Lie group. This follows from the fact that the unit circle is a compact abelian Lie group (when identified with the unit complex numbers with multiplication). Group multiplication on the torus is then defined by coordinate-wise multiplication.
Toroidal groups play an important part in the theory of compact Lie groups. This is due in part to the fact that in any compact Lie group G one can always find a maximal torus; that is, a closed subgroup which is a torus of the largest possible dimension. Such maximal tori T have a controlling role to play in theory of connected G.
Automorphisms of T are easily constructed from automorphisms of the lattice Zn, which are classified by integral matrices M of size n×n which are invertible with integral inverse; these are just the integral M of determinant +1 or −1. Making M act on Rn in the usual way, one has the typical toral automorphism on the quotient.
The fundamental group of an n-torus is a free abelian group of rank n. The k-th homology group of an n-torus is a free abelian group of rank n choose k. It follows that the Euler characteristic of the n-torus is 0 for all n. The cohomology ring H•(Tn,Z) can be identified with the exterior algebra over the Z–module Zn whose generators are the duals of the n nontrivial cycles.
Configuration space
The configuration space of 2 not necessarily distinct points on the circle is the orbifold quotient of the 2-torus, T2 / S2, which is the Möbius strip.
As the n-torus is the n-fold product of the circle, the n-torus is the configuration space of n ordered, not necessarily distinct points on the circle. Symbolically, Tn = (S1)n. The configuration space of unordered, not necessarily distinct points is accordingly the orbifold Tn / Sn, which is the quotient of the torus by the symmetric group on n letters (by permuting the coordinates).
For n = 2, the quotient is the Möbius strip, the edge corresponding to the orbifold points where the two coordinates coincide. For n = 3 this quotient may be described as a solid torus with cross-section an equilateral triangle, with a twist; equivalently, as a triangular prism whose top and bottom faces are connected with a ⅓ twist (120°): the 3-dimensional interior corresponds to the points on the 3-torus where all 3 coordinates are distinct, the 2-dimensional face corresponds to points with 2 coordinates equal and the 3rd different, while the 1-dimensional edge corresponds to points with all 3 coordinates identical.
These orbifolds have found significant applications to music theory in the work of Dmitri Tymoczko and collaborators (Felipe Posada and Michael Kolinas, et al.), being used to model musical triads.[5][6]
Flat torus
The flat torus is a specific embedding of the familiar 2-torus into Euclidean 4-space or higher dimensions. Its surface has zero Gaussian curvature everywhere. Its surface is “flat” in the same sense that the surface of a cylinder is “flat”. In 3 dimensions one can bend a flat sheet of paper into a cylinder without stretching the paper, but you cannot then bend this cylinder into a torus without stretching the paper. In 4 dimensions one can (mathematically).
A simple 4-d Euclidean embedding is as follows: <x,y,z,w> = <R cos u, R sin u, P cos v, P sin v> where R and P are constants determining the aspect ratio. It is diffeomorphic to a regular torus but not isometric. It can not be isometrically embedded into Euclidean 3-space. Mapping it into 3-space requires you to “bend” it, in which case it looks like a regular torus, for example, the following map <x,y,z> = <(R + P sin v)cos u, (R + P sin v)sin u, P cos v>.
A flat torus partitions the 3-sphere into two congruent solid tori subsets with the aforsaid flat torus surface as their common boundary.

A stereographic projection of a Clifford torus performing a simple rotation through the xz-plane. |
n-fold torus
In the theory of surfaces the term n-torus has a different meaning. Instead of the product of n circles, they use the phrase to mean the connected sum of n 2-dimensional tori. To form a connected sum of two surfaces, remove from each the interior of a disk and “glue” the surfaces together along the disks’ boundary circles. To form the connected sum of more than two surfaces, sum two of them at a time until they are all connected together. In this sense, an n-torus resembles the surface of n doughnuts stuck together side by side, or a 2-dimensional sphere with n handles attached.
An ordinary torus is a 1-torus, a 2-torus is called a double torus, a 3-torus a triple torus, and so on. The n-torus is said to be an “orientable surface” of “genus” n, the genus being the number of handles. The 0-torus is the 2-dimensional sphere.
The classification theorem for surfaces states that every compact connected surface is either a sphere, an n-torus with n > 0, or the connected sum of n projective planes (that is, projective planes over the real numbers) with n > 0.

|

|
Toroidal polyhedra
A toroidal polyhedron with 6×4=24 quadrilateral faces.
Polyhedra with the topological type of a torus are called toroidal polyhedra, and satisfy a modified version of the polyhedron formula, E − F − V = 0.
The term “toroidal polydron” is also used for higher genus polyhedra and for immersions of toroidal polyhedra.
| This section requires expansion. |
Automorphisms
The homeomorphism group (or the subgroup of diffeomorphisms) of the torus is studied in geometric topology. Its mapping class group (the group of connected components) is isomorphic to the group GL(n, Z) of invertible integer matrices, and can be realized as linear maps on the universal covering space  that preserve the standard lattice
that preserve the standard lattice  (this corresponds to integer coefficients) and thus descend to the quotient.
(this corresponds to integer coefficients) and thus descend to the quotient.
At the level of homotopy and homology, the mapping class group can be identified as the action on the first homology (or equivalently, first cohomology, or on the fundamental group, as these are all naturally isomorphic; note also that the first cohomology group generates the cohomology algebra):
Since the torus is an Eilenberg-MacLane space K(G, 1), its homotopy equivalences, up to homotopy, can be identified with automorphisms of the fundamental group); that this agrees with the mapping class group reflects that all homotopy equivalences can be realized by homeomorphisms – every homotopy equivalence is homotopic to a homeomorphism – and that homotopic homeomorphisms are in fact isotopic (connected through homeomorphisms, not just through homotopy equivalences). More tersely, the map 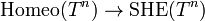 is 1-connected (isomorphic on path-components, onto fundamental group). This is a “homeomorphism reduces to homotopy reduces to algebra” result.
is 1-connected (isomorphic on path-components, onto fundamental group). This is a “homeomorphism reduces to homotopy reduces to algebra” result.
Thus the short exact sequence of the mapping class group splits (an identification of the torus as the quotient of 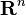 gives a splitting, via the linear maps, as above):
gives a splitting, via the linear maps, as above):
so the homeomorphism group of the torus is a semidirect product, 
The mapping class group of higher genus surfaces is much more complicated, and an area of active research.
Coloring a torus
If a torus is divided into regions, then it is always possible to color the regions with no more than seven colors so that neighboring regions have different colors. (Contrast with the four color theorem for the plane.)
Cutting a torus
A standard torus (specifically, a ring torus) can be cut with n planes into at most 16(n3 + 3n2 + 8n) parts, integer sequence A003600.[7] The initial terms of this sequence are 1, 2, 6, 13, for n starting from 0.
See also
Notes
- ^ Harold A. Stein … (2002). Fitting guide for rigid and soft contact lenses : a practical approach. St. Louis: Mosby. p. 16. ISBN 9780323014403. http://books.google.com/?id=GGoNQzt3I_IC&pg=PA16&lpg=PA16&dq=torus+Latin+word+for+a+cushion+of+this+shape.
- ^ http://www.geom.uiuc.edu/zoo/toptype/torus/standard/eqns.html
- ^ Weisstein, Eric W., “Torus” from MathWorld.
- ^ “Oxford English Dictionary Online”. poloidal. Oxford University Press. http://dictionary.oed.com/cgi/entry/50183023?single=1&query_type=word&queryword=poloidal&first=1&max_to_show=10. Retrieved 2007-08-10.
- ^ Tymoczko, Dmitri (7 July 2006). “The Geometry of Musical Chords”. Science 313 (5783): 72–74. doi:10.1126/science.1126287. PMID 16825563. http://www.brainmusic.org/EducationalActivitiesFolder/Tymoczko_chords2006.pdf
- ^ Tony Phillips, Tony Phillips’ Take on Math in the Media, American Mathematical Society, October 2006
- ^ Weisstein, Eric W., “Torus Cutting” from MathWorld.
References
- NOCIONES DE GEOMETRIA ANALITICA Y ALGEBRA LINEAL, ISBN 9789701065969, Author: KOZAK ANA MARIA, POMPEYA PASTORELLI SONIA, VERDANEGA PEDRO EMILIO, Editorial: MCGRAW-HILL, Edition 2007, 744 pages, language; spanish
- Allen Hatcher. Algebraic topology. Cambridge University Press, 2002. ISBN 0-521-79540-0.
- V.V. Nikulin, I.R.Shafarevich. Geometries and Groups. Springer, 1987. ISBN 3540152814, ISBN 9783540152811.
- http://www.mathcurve.com/surfaces/tore/tore.shtml
- “Tore (notion géométrique)” at Encyclopédie des Formes Mathématiques Remarquables
External links
| Wikimedia Commons has media related to: Torus |
- Creation of a torus at cut-the-knot
- “4D torus” Fly-through cross-sections of a four dimensional torus.
- “Relational Perspective Map” Visualizing high dimensional data with flat torus.
- “Torus Games” Free downloadable games for Windows and Mac OS X that highlight the topology of a torus.
- Polydos
This information originally retrieved from http://en.wikipedia.org/wiki/Torus
on Wednesday 24th August 2011 12:48 pm EDT
Now edited and maintained by ManufacturingET.org