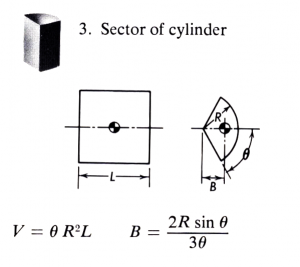
Create a model of the cylinder sector shown. Build the model such that no matter what dimensions are given for L and Theta, the model will oriented with the Absolute CSYS at its center of mass. Hint: Use expressions, use symmetrical extrusion (ignore note for NX11—>) (Note: If you are not using Theta as an argument for one of the trig functions, use RADIANS(Theta) to return Theta as radians. This is necessary even if Theta has units of radians).
Verify that the center of mass is:
Xcbar, Ycbar, Zcbar = -0.00000000000, 0.00000000000, 0.00000000000
For several values of R, L, and Theta.
Example:
Radius = 1
Theta = Pi()/4
B = .6002108774
See also:
http://www.eng.auburn.edu/~marghitu/MECH2110/C_3.pdf