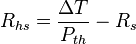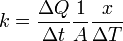Thermal Conductivity

In physics, thermal conductivity, k, is the property of a material’s ability to conduct heat. It appears primarily in Fourier’s Law for heat conduction.

Heat transfer across materials of high thermal conductivity occurs at a faster rate than across materials of low thermal conductivity. Correspondingly materials of high thermal conductivity are widely used in heat sink applications and materials of low thermal conductivity are used as thermal insulation.

Thermal conductivity of materials is temperature dependent. In general, materials become more conductive to heat as the average temperature increases.^[1]

The reciprocal of thermal conductivity is thermal resistivity.

Contents 1 Units of thermal conductivity 2 Measurement 3 Definitions 3.1 Conductance 3.2 Resistance 3.3 Transmittance 4 Influencing factors 4.1 Temperature 4.2 Material phase 4.3 Material structure 4.4 Electrical conductivity 4.5 Convection 5 Experimental values 6 Physical origins 6.1 Lattice waves 7 Equations 8 See also 9 References 10 Further reading 11 External links

Units of thermal conductivity

In the International System of Units (SI), thermal conductivity is measured in watts per meter kelvin (W/(m·K)).

In the imperial system of measurement thermal conductivity is measured in Btu/(hr·ft⋅F) where 1 Btu/(hr·ft⋅F) = 1.730735 W/(m·K). [Perry’s Chemical Engineers’ Handbook, 7th Edition, Table 1-4]

Other units which are closely related to the thermal conductivity are in common use in the construction and textile industries. The construction industry makes use of units such as the R-Value (resistance value) and the U-Value (thermal transmittance). Although related to the thermal conductivity of a product R and U-values are dependent on the thickness of a product.

Likewise the textile industry has several units including the Tog and the Clo which express thermal resistance of a material in a way analogous to the R-values used in the construction industry.

Note: R-Values and U-Values quoted in the US (based on the imperial units of measurement) do not correspond with and are not compatible with those used in Europe (based on the SI units of measurement).

Measurement

There are a number of ways to measure thermal conductivity. Each of these is suitable for a limited range of materials, depending on the thermal properties and the medium temperature. There is a distinction between steady-state and transient techniques.

In general, steady-state techniques are useful when the temperature of the material does not change with time. This makes the signal analysis straightforward (steady state implies constant signals). The disadvantage is that a well-engineered experimental setup is usually needed. The Divided Bar (various types) is the most common device used for consolidated rock samples.

The transient techniques perform a measurement during the process of heating up. Their advantage is quicker measurements. Transient methods are usually carried out by needle probes. A method described by Angstrom involves rapidly cycling the temperature from hot to cold and back and measuring the temperature change as the heat propogates along a thin strip of material in a vacuum.

Definitions

The reciprocal of thermal conductivity is thermal resistivity, usually measured in kelvin-meters per watt (K·m·W⁻¹). When dealing with a known amount of material, its thermal conductance and the reciprocal property, thermal resistance, can be described. Unfortunately, there are differing definitions for these terms.

Conductance

For general scientific use, thermal conductance is the quantity of heat that passes in unit time through a plate of particular area and thickness when its opposite faces differ in temperature by one kelvin. For a plate of thermal conductivity k, area A and thickness L this is kA/L, measured in W·K⁻¹ (equivalent to: W/°C). Thermal conductivity and conductance are analogous to electrical conductivity (A·m⁻¹·V⁻¹) and electrical conductance (A·V⁻¹).

There is also a measure known as heat transfer coefficient: the quantity of heat that passes in unit time through unit area of a plate of particular thickness when its opposite faces differ in temperature by one kelvin. The reciprocal is thermal insulance. In summary:

• thermal conductance = kA/L, measured in W·K⁻¹
  • thermal resistance = L /(kA), measured in K·W⁻¹ (equivalent to: °C/W)
• heat transfer coefficient = k/L, measured in W·K⁻¹·m⁻²
  • thermal insulance = L /k, measured in K·m²·W⁻¹.

The heat transfer coefficient is also known as thermal admittance

Resistance

When thermal resistances occur in series, they are additive. So when heat flows through two components each with a resistance of 1 °C/W, the total resistance is 2 °C/W.

A common engineering design problem involves the selection of an appropriate sized heat sink for a given heat source. Working in units of thermal resistance greatly simplifies the design calculation. The following formula can be used to estimate the performance:

where:

• R_hs is the maximum thermal resistance of the heat sink to ambient, in °C/W
• ΔT is the temperature difference (temperature drop), in °C
• P_th is the thermal power (heat flow), in watts
• R_s is the thermal resistance of the heat source, in °C/W

For example, if a component produces 100 W of heat, and has a thermal resistance of 0.5 °C/W, what is the maximum thermal resistance of the heat sink? Suppose the maximum temperature is 125 °C, and the ambient temperature is 25 °C; then the ΔT is 100 °C. The heat sink’s thermal resistance to ambient must then be 0.5 °C/W or less.

Transmittance

A third term, thermal transmittance, incorporates the thermal conductance of a structure along with heat transfer due to convection and radiation. It is measured in the same units as thermal conductance and is sometimes known as the composite thermal conductance. The term U-value is another synonym.

Influencing factors

Temperature

The effect of temperature on thermal conductivity is different for metals and nonmetals. In metals conductivity is primarily due to lattice vibrations and free electron, however, free electrons play a dominant role. Therefore any increase in temperature increases the lattice vibrations but affects the movement of free electrons adversly thereby decreasing the conductivity. On the other hand conductivity in nonmetals is only due to lattice vibrations which increases with increasing temperature, and so the conductivity of nonmetals increases with increasing temperature.

Material phase

When a material undergoes a phase change from solid to liquid or from liquid to gas the thermal conductivity may change. An example of this would be the change in thermal conductivity that occurs when ice (thermal conductivity of 2.18 W/(m·K) at 0 °C) melts into liquid water (thermal conductivity of 0.58 W/(m·K) at 0 °C).

Material structure

Pure crystalline substances exhibit very different thermal conductivities along different crystal axes, due to differences in phonon coupling along a given crystal axis. Sapphire is a notable example of variable thermal conductivity based on orientation and temperature, with 35 W/(m·K) along the c-axis and 32 W/(m·K) along the a-axis.^[2]

Electrical conductivity

In metals, thermal conductivity approximately tracks electrical conductivity according to the Wiedemann-Franz law, as freely moving valence electrons transfer not only electric current but also heat energy. However, the general correlation between electrical and thermal conductance does not hold for other materials, due to the increased importance of phonon carriers for heat in non-metals. As shown in the table below, highly electrically conductive silver is less thermally conductive than diamond, which is an electrical insulator.

Convection

Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials function simply by having a large number of gas-filled pockets which prevent large-scale convection. Examples of these include expanded and extruded polystyrene (popularly referred to as “styrofoam”) and silica aerogel. Natural, biological insulators such as fur and feathers achieve similar effects by dramatically inhibiting convection of air or water near an animal’s skin.

Light gases, such as hydrogen and helium typically have high thermal conductivity. Dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity. An exception, sulfur hexafluoride, a dense gas, has a relatively high thermal conductivity due to its high heat capacity. Argon, a gas denser than air, is often used in insulated glazing (double paned windows) to improve their insulation characteristics.

Experimental values

Thermal conductivity is important in building insulation and related fields. However, materials used in such trades are rarely subjected to chemical purity standards. Several construction materials’ k values are listed below. These should be considered approximate due to the uncertainties related to material definitions. In the opposite end of the spectrum, solutions for computer cooling usually use high thermal capacity materials such as silver, copper and aluminium, to cool down specific components.

The following table is meant as a small sample of data to illustrate the thermal conductivity of various types of substances. For more complete listings of measured k-values, see the references.

This is a list of approximate values of thermal conductivity, k, for some common materials. Please consult the list of thermal conductivities for more accurate values, references and detailed information.

Material	Thermal conductivity [W/(m·K)]
Silica Aerogel	0.004 – 0.04
Air	0.025
Wood	0.04 – 0.4
Hollow Fill Fibre Insulation	0.042
Alcohols and oils	0.1 – 0.21
Polypropylene	0.25 [3]
Mineral oil	0.138
Rubber	0.16
LPG	0.23 – 0.26
Cement, Portland	0.29
Epoxy (silica-filled)	0.30
Epoxy (unfilled)	0.12 – 0.177 [4][5]
Water (liquid)	0.6
Thermal grease	0.7 – 3
Thermal epoxy	1 – 7
Glass	1.1
Soil	1.5
Concrete, stone	1.7
Ice	2
Sandstone	2.4
Mercury	8.3
Stainless steel	12.11 ~ 45.0
Lead	35.3
Aluminium	237 (pure) 120—180 (alloys)
Gold	318
Copper	401
Silver	429
Diamond	900 – 2320
Graphene	(4840±440) – (5300±480)

Physical origins

Heat flux is exceedingly difficult to control and isolate in a laboratory setting. Thus at the atomic level, there are no simple, correct expressions for thermal conductivity. Atomically, the thermal conductivity of a system is determined by how atoms composing the system interact. There are two different approaches for calculating the thermal conductivity of a system.

• The first approach employs the Green-Kubo relations. Although this employs analytic expressions which in principle can be solved, calculating the thermal conductivity of a dense fluid or solid using this relation requires the use of molecular dynamics computer simulation.

• The second approach is based upon the relaxation time approach. Due to the anharmonicity within the crystal potential, the phonons in the system are known to scatter. There are three main mechanisms for scattering:
  • Boundary scattering, a phonon hitting the boundary of a system;
  • Mass defect scattering, a phonon hitting an impurity within the system and scattering;
  • Phonon-phonon scattering, a phonon breaking into two lower energy phonons or a phonon colliding with another phonon and merging into one higher energy phonon.

Lattice waves

Heat transport in both glassy and crystalline dielectric solids occurs through elastic vibrations of the lattice (phonons). This transport is limited by elastic scattering of acoustic phonons by lattice defects. These predictions were confirmed by the experiments of Chang and Jones on commercial glasses and glass ceramics, where mean free paths were limited by “internal boundary scattering” to length scales of 10⁻² cm to 10⁻³ cm. ^[6][7]

The phonon mean free path has been associated directly with the effective relaxation length for processes without directional correlation. Thus, if V_g  is the group velocity of a phonon wave packet, then the relaxation length is defined as:

where t is the characteristic relaxation time. Since longitudinal waves have a much greater phase velocity than transverse waves, V_long is much greater than V_trans, and the relaxation length or mean free path of longitudinal phonons will be much greater. Thus, thermal conductivity will be largely determined by the speed of longitudinal phonons. ^[6][8]

Regarding the dependence of wave velocity on wavelength or frequency (dispersion), low-frequency phonons of long wavelength will be limited in relaxation length by elastic Rayleigh scattering. This type of light scattering form small particles is proportional to the fourth power of the frequency. For higher frequencies, the power of the frequency will decrease until at highest frequencies scattering is almost frequency independent. Similar arguments were subsequently generalized to many glass forming substances using Brillouin scattering. ^{[9][10] [11] [12]}

Equations

First, we define heat conduction, H:

where 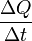is the rate of heat flow, k is the thermal conductivity, A is the total cross sectional area of conducting surface, ΔT is temperature difference, and x is the thickness of conducting surface separating the two temperatures. Dimension of thermal conductivity = M¹L¹T⁻³K⁻¹

Rearranging the equation gives thermal conductivity:

(Note: ΔT / x is the temperature gradient)

I.E. It is defined as the quantity of heat, ΔQ, transmitted during time Δt through a thickness x, in a direction normal to a surface of area A, per unit area of A, due to a temperature difference ΔT, under steady state conditions and when the heat transfer is dependent only on the temperature gradient.

Alternatively, it can be thought of as a flux of heat (energy per unit area per unit time) divided by a temperature gradient (temperature difference per unit length)

See also

References

Further reading

• Callister, William (2003). “Appendix B”. Materials Science and Engineering – An Introduction. John Wiley & Sons, INC. pp. 757. ISBN 0-471-22471-5. 
• Halliday, David; Resnick, Robert; & Walker, Jearl(1997). Fundamentals of Physics (5th ed.). John Wiley and Sons, INC., NY ISBN 0-471-10558-9.
• Srivastava G. P (1990), “The Physics of Phonons.” Adam Hilger, IOP Publishing Ltd, Bristol.
• TM 5-852-6 AFR 88-19, Volume 6 (Army Corp of Engineers publication)

External links

• Table with the Thermal Conductivity of the Elements
• Calculation of the Thermal Conductivity of Glass Calculation of the Thermal Conductivity of Glass at Room Temperature from the Chemical Composition
• Viscosity and Thermal Conductivity Equations for Nitrogen, Oxygen, Argon, and Air
• Conversion of thermal conductivity values for many unit systems