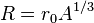Nucleus

 

The nucleus is the very dense region consisting of nucleons (protons and neutrons) at the center of an atom. Almost all of the mass in an atom is made up from the protons and neutrons in the nucleus, with a very small contribution from the orbiting electrons. It was discovered in 1911, as a result of Ernest Rutherford‘s interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The proton–neutron model of nucleus was proposed by Dmitry Ivanenko in 1932.^{[citation needed]}

The diameter of the nucleus is in the range of 1.75 fm (femtometre) (1.75×10⁻¹⁵ m) for hydrogen (the diameter of a single proton)^[1] to about 15 fm for the heaviest atoms, such as uranium. These dimensions are much smaller than the diameter of the atom itself (nucleus + electronic cloud), by a factor of about 23,000 (uranium) to about 145,000 (hydrogen).

The branch of physics concerned with studying and understanding the atomic nucleus, including its composition and the forces which bind it together, is called nuclear physics.

Contents 1 Introduction 1.1 Etymology 1.2 Nuclear makeup 2 Protons and neutrons 3 Forces 4 Halo nuclei and strong force range limits 5 Nuclear models 5.1 Liquid drop models 5.2 Shell models and other quantum models 5.3 Consistency between models 6 See also 7 Notes 8 References 9 External links

Introduction

Etymology

The term nucleus is from the Latin word nucleus (“nut”). In 1844, Michael Faraday used the term to refer to the “central point of an atom”. The modern atomic meaning was proposed by Ernest Rutherford in 1912.^[2] The adoption of the term “nucleus” to atomic theory, however, was not immediate. In 1916, for example, Gilbert N. Lewis stated, in his famous article The Atom and the Molecule, that “the atom is composed of the kernel and an outer atom or shell“^[3]

Nuclear makeup

The nucleus of an atom consists of protons and neutrons (two types of baryons) bound by the nuclear force (also known as the residual strong force). These baryons are further composed of subatomic fundamental particles known as quarks bound by the strong interaction. Which chemical element an atom represents is determined by the number of protons in the nucleus. Each proton carries a single positive charge, and the total electrical charge of the nucleus is spread fairly uniformly throughout its body, with a fall-off at the edge.

Major exceptions to this rule are the light elements hydrogen and helium, where the charge is concentrated most highly at the single central point (without a volume of uniform charge), as would be expected for fermions (in this case, protons) in 1s states without orbital angular momentum.^[4]

As each proton carries a unit of charge, the charge distribution is indicative of the proton distribution. The neutron distribution probably is similar.^[4]

Protons and neutrons

Protons and neutrons are fermions, with different values of the isospin quantum number,^{[dubious – discuss]} so two protons and two neutrons can share the same space wave function since they are not identical quantum entities. They sometimes are viewed as two different quantum states of the same particle, the nucleon.^[5][6] Two fermions, such as two protons, or two neutrons, or a proton + neutron (the deuteron) can exhibit bosonic behavior when they become loosely bound in pairs.

In the rare case of a hypernucleus, a third baryon called a hyperon, with a different value of the strangeness quantum number can also share the wave function. However, the latter type of nuclei are extremely unstable and are not found on Earth except in high energy physics experiments.

The neutron has a positively charged core of radius ≈ 0.3 fm surrounded by a compensating negative charge of radius between 0.3 fm and 2 fm. The proton has an approximately exponentially decaying positive charge distribution with a mean square radius of about 0.8 fm.^[7]

Forces

Nuclei are bound together by the residual strong force (nuclear force). The residual strong force is minor residuum of the strong interaction which binds quarks together to form protons and neutrons. This force is much weaker between neutrons and protons because it is mostly neutralized within them, in the same way that electromagnetic forces between neutral atoms (such as van der Waals forces that act between two inert gas atoms) are much weaker than the electromagnetic forces that hold the parts of the atoms internally together (for example, the forces that hold the electrons in an inert gas atom bound to its nucleus).

The nuclear force is highly attractive at the distance of typical nucleon separation, and this overwhelms the repulsion between protons which is due to the electromagnetic force, thus allowing nuclei to exist. However, because the residual strong force has a limited range because it decays quickly with distance (see Yukawa potential), only nuclei smaller than a certain size can be completely stable. The largest known completely stable (e.g., stable to alpha, beta, and gamma decay) nucleus is lead-208 which contains a total of 208 nucleons (126 neutrons and 82 protons). Nuclei larger than this maximal size of 208 particles are unstable and (as a trend) become increasingly short-lived with larger size, as the number of neutrons and protons which compose them increases beyond this number. However, bismuth-209 is also stable to beta decay and has the longest half-life to alpha decay of any known isotope, estimated at a billion times longer than the age of the universe.

The residual strong force is effective over a very short range (usually only a few fermis; roughly one or two nucleon diameters) and causes an attraction between any pair of nucleons. For example, between protons and neutrons to form [NP] deuteron, and also between protons and protons, and neutrons and neutrons. It also is effective for the stability of one 3-body nucleon system [PNP], helium-3, while the triton [NPN] is unstable and decays to helium-3.

Halo nuclei and strong force range limits

The effective absolute limit of the range of the strong force is represented by halo nuclei such as lithium-11 or boron-14, in which dineutrons, or other collections of neutrons, orbit at distances of about ten fermis (roughly similar to the 8 fermi radius of the nucleus of uranium-238). These nuclei are not maximally dense. Halo nuclei form at the extreme edges of the chart of the nuclides—the neutron drip line and proton drip line—and are all unstable with short half-lives, measured in milliseconds; for example, lithium-11 has a half-life of less than 8.6 milliseconds.

Halos in effect represent an excited state with nucleons in an outer quantum shell which has unfilled energy levels “below” it (both in terms of radius and energy). The halo may be made of either neutrons [NN, NNN] or protons [PP, PPP]. Examples: Nuclei which have a single neutron halo include 11Be and 19C. A two-neutron halo is exhibited by ⁶He, ¹¹Li, ¹⁷B, ¹⁹B and ²²C. Two-neutron halo nuclei break into three fragments, never two, and are called Borromean because of this behavior (referring to a system of three interlocked rings in which breaking any ring frees both of the others). ⁸He and ¹⁴Be both exhibit a four-neutron halo. Nuclei which have a proton halo include ⁸B and ²⁶P. A two-proton halo is exhibited by ¹⁷Ne and ²⁷S. Proton halos are expected to be more rare and unstable than the neutron examples, because of the repulsive electromagnetic forces of the excess proton(s).

Nuclear models

There are many different historical models of the atomic nucleus, none of which to this day completely explains experimental data on nuclear structure. A useful review of 37 known models of the atomic nucleus is provided by Cook.^[8]

The nuclear radius (R) is considered to be one of the basic things that any model must predict. For stable nuclei (not halo nuclei or other unstable distorted nuclei) the nuclear radius is roughly proportional to the cube root of the mass number (A) of the nucleus, and particularly in nuclei containing many nucleons, as they arrange in more spherical configurations:

The stable nucleus has approximately a constant density and therefore the nuclear radius R can be approximated by the following formula,

where A = Atomic mass number (the number of protons, Z, plus the number of neutrons, N) and r₀ = 1.25 fm = 1.25 × 10⁻¹⁵ m. In this equation, the constant r₀ varies by 0.2 fm, depending on the nucleus in question, but this is less than 20% change from a constant.^[9]

In other words, packing protons and neutrons in the nucleus gives approximately the same total size result as packing hard spheres of a constant size (like marbles) into a tight spherical or semi-spherical bag (some stable nuclei are not quite spherical, but are known to be prolate).^{[citation needed]}

Liquid drop models

Early models of the nucleus viewed the nucleus as a rotating liquid drop. In this model, the trade-off of long-range electromagnetic forces and relatively short-range nuclear forces, together cause behavior which resembled surface tension forces in liquid drops of different sizes. This formula is successful at explaining many important phenomena of nuclei, such as their changing amounts of binding energy as their size and composition changes (see semi-empirical mass formula), but it does not explain the special stability which occurs when nuclei have special “magic numbers” of protons or neutrons.

Shell models and other quantum models

A number of models for the nucleus have also been proposed in which nucleons occupy orbitals, much like the atomic orbitals in atomic physics theory. These wave models imagine nucleons to be either sizeless point particles in potential wells, or else probability waves as in the “optical model”, frictionlessly orbiting at high speed in potential wells.

In these models, the nucleons may occupy orbitals in pairs, due to being fermions, but the exact nature and capacity of nuclear shells differs from those of electrons in atomic orbitals, primarily because the potential well in which the nucleons move (especially in larger nuclei) is quite different from the central electromagnetic potential well which binds electrons in atoms. Some resemblance to atomic orbital models may be seen in a small atomic nucleus like that of helium-4, in which the two protons and two neutrons separately occupy 1s orbitals analogous to the 1s orbital for the two electrons in the helium atom, and achieve unusual stability for the same reason. Nuclei with 5 nucleons are all extremely unstable and short-lived, yet, helium-3, with 3 nucleons, is very stable even with lack of a closed 1s orbital shell. Another nucleus with 3 nucleons, the triton hydrogen-3 is unstable and will decay into helium-3 when isolated. Weak nuclear stability with 2 nucleons {NP} in the 1s orbital is found in the deuteron hydrogen-2, with only one nucleon in each of the proton and neutron potential wells. While each nucleon is a fermion, the {NP} deuteron is a boson and thus does not follow Pauli Exclusion for close packing within shells. Lithium-6 with 6 nucleons is highly stable without a closed second 1p shell orbital. For light nuclei with total nucleon numbers 1 to 6 only those with 5 do not show some evidence of stability. Observations of beta-stability of light nuclei outside closed shells indicate that nuclear stability is much more complex than simple closure of shell orbitals with magic numbers of protons and neutrons.

For larger nuclei, the shells occupied by nucleons begin to differ significantly from electron shells, but nevertheless, present nuclear theory does predict the magic numbers of filled nuclear shells for both protons and neutrons. The closure of the stable shells predicts unusually stable configurations, analogous to the noble group of nearly-inert gases in chemistry. An example is the stability of the closed shell of 50 protons, which allows tin to have 10 stable isotopes, more than any other element. Similarly, the distance from shell-closure explains the unusual instability of isotopes which have far from stable numbers of these particles, such as the radioactive elements 43 (technetium) and 61 (promethium), each of which is preceded and followed by 17 or more stable elements.

There are however problems with the shell model when an attempt is made to account for nuclear properties well away from closed shells. This has led to complex post hoc distortions of the shape of the potential well to fit experimental data, but the question remains whether these mathematical manipulations actually correspond to the spatial deformations in real nuclei. Problems with the shell model have led some to propose realistic two-body and three-body nuclear force effects involving nucleon clusters and then build the nucleus on this basis. Two such cluster models are the Close-Packed Spheron Model of Linus Pauling and the 2D Ising Model of MacGregor.^[8]

Consistency between models

As with the case of superfluid liquid helium, atomic nuclei are an example of a state in which both (1) “ordinary” particle physical rules for volume and (2) non-intuitive quantum mechanical rules for a wave-like nature apply. In superfluid helium, the helium atoms have volume, and essentially “touch” each other, yet at the same time exhibit strange bulk properties, consistent with a Bose-Einstein condensation. The latter reveals that they also have a wave-like nature and do not exhibit standard fluid properties, such as friction. For nuclei made of hadrons which are fermions, the same type of condensation does not occur, yet nevertheless, many nuclear properties can only be explained similarly by a combination of properties of particles with volume, in addition to the frictionless motion characteristic of the wave-like behavior of objects trapped in Schrödinger quantum orbitals.

See also

Notes

References

• N.D. Cook (2010). Models of the Atomic Nucleus (2nd ed.). Springer. ISBN 978-3-642-14736-4. 

External links

• The Nucleus – a chapter from an online textbook
• The LIVEChart of Nuclides – IAEA in Java or HTML
• Article on the “nuclear shell model,” giving nuclear shell filling for the various elements. Accessed Sept. 16, 2009.

v · d · eParticles in physics Elementary Fermions Quarks u · d · c · s · t · b Leptons e−  · e+  · μ−  · μ+  · τ−  · τ+  · ν e · ν e · ν μ · ν μ · ν τ · ν τ Bosons Gauge γ · g · W±  · Z Others Ghosts Hypothetical Superpartners Gauginos Gluino · Gravitino Others Axino · Chargino · Higgsino · Neutralino  · Sfermion Others A0 · Dilaton · G · H0  · J · Tachyon · X · Y · W’ · Z’ · Sterile neutrino Composite Hadrons Baryons / Hyperons N (p · n) · Δ · Λ · Σ · Ξ · Ω Mesons / Quarkonia π · ρ · η · η′ · φ · ω · J/ψ · ϒ · θ · K · B · D · T Others Atomic nuclei · Atoms · Diquarks · Exotic atoms (Positronium · Muonium · Onia) · Superatoms · Molecules Hypothetical Exotic hadrons Exotic baryons Dibaryon · Pentaquark Exotic mesons Glueball · Tetraquark Others Mesonic molecule · Pomeron Quasiparticles Davydov soliton · Exciton · Hole · Magnon · Phonon · Plasmaron · Plasmon · Polariton · Polaron · Roton · Trion Lists List of particles · List of quasiparticles · List of baryons · List of mesons · Timeline of particle discoveries Wikipedia books Book:Hadronic Matter · Book:Particles of the Standard Model · Book:Leptons · Book:Quarks

v · d · eNuclear technology Science Chemistry · Engineering · Physics · Atomic nucleus · Fission · Fusion · Radiation (ionizing) Fuel Deuterium · Fertile material · Fissile · Isotope separation · Plutonium · Thorium · Tritium · Uranium (enriched • depleted) Neutron Activation · Capture · Cross-section · Fast · Fusion · Generator · Poison · Radiation · Reflector · Temp · Thermal Reactors Fission reactorsby moderator Water Boiling (BWR · ABWR) · Heavy (CANDU · PHWR · SGHWR) · Natural (NFR) · Pressurized (PWR · VVER · EPR) · Supercritical (SCWR) Carbon Advanced gas-cooled (AGR) · Magnox · Pebble bed (PBMR) · RBMK · UHTREX · Very high temperature (VHTR) FLiBe Molten salt (MSR) None (Fast) Breeder (FBR) · Integral (IFR) · Liquid-metal-cooled (LMFR) · SSTAR · Traveling Wave (TWR) Generation IV by coolant: (Gas (GFR) · Lead (LFR) · Sodium (SFR)) Fusion reactors by confinement Magnetic Field-reversed configuration · Levitated dipole · Reversed field pinch · Spheromak · Stellarator · Tokamak Inertial Bubble fusion (acoustic) · Fusor (electrostatic) · Laser-driven · Magnetized target · Z-pinch Other Dense plasma focus · Migma · Muon-catalyzed · Polywell · Pyroelectric List of nuclear reactors Power Nuclear power plant · By country · Economics · Fusion · Isotope thermoelectric (RTG) · Propulsion (rocket) · Safety Medicine Imaging byradiation Gamma camera Scintigraphy · Positron emission (PET) · Single photon emission (SPECT) X-ray Projectional radiography · Computed tomography Therapy Boron neutron capture (BNCT) · Brachytherapy · Proton · Radiation · Tomotherapy Weapon Topics Arms race · Delivery · Design · Explosion (effects) · History · Proliferation · Testing (underground) · Warfare · Yield (TNTe) Lists Popular culture · States · Tests · Treaties · Weapon-free zones · Weapons Waste Products Actinide: (Reprocessed uranium · Reactor-grade plutonium · Minor actinide) · Activation · Fission (LLFP) Disposal Fuel cycle · HLW · LLW · Repository · Reprocessing · Spent fuel (pool • cask) · Transmutation Debate Anti-nuclear movement · Nuclear power debate · Nuclear weapons debate · Uranium mining debate · Nuclear power phase-out