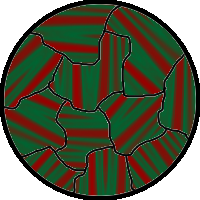
Ferromagnetism is the basic mechanism by which certain materials (such as iron) form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished. Ferromagnetism (including ferrimagnetism) is the strongest type; it is the only type strong enough to be felt, and is usually responsible for the common phenomena of magnetism encountered in everyday life. Other substances respond weakly to magnetic fields with two other types of magnetism, paramagnetism and diamagnetism. An everyday example of ferromagnetism is a refrigerator magnet used to hold notes on a refrigerator door. The attraction between a magnet and ferromagnetic material is “the quality of magnetism first apparent to the ancient world, and to us today,” according to a classic text on ferromagnetism.[1]
All permanent magnets (materials that can be magnetized by an external magnetic field and which remain magnetized after the external field is removed) are either ferromagnetic or ferrimagnetic, as are other materials that are noticeably attracted to them.
Contents |
History and distinction from ferrimagnetism
Historically, the term ferromagnet was used for any material that could exhibit spontaneous magnetization: a net magnetic moment in the absence of an external magnetic field. This general definition is still in common use. More recently, however, different classes of spontaneous magnetization have been identified[citation needed] when there is more than one magnetic ion per primitive cell of the material, leading to a stricter definition of “ferromagnetism” that is often used to distinguish it from ferrimagnetism.[citation needed] In particular, a material is “ferromagnetic” in this narrower sense only if all of its magnetic ions add a positive contribution to the net magnetization. If some of the magnetic ions subtract from the net magnetization (if they are partially anti-aligned), then the material is “ferrimagnetic”.[citation needed] If the moments of the aligned and anti-aligned ions balance completely so as to have zero net magnetization, despite the magnetic ordering, then it is an antiferromagnet. All of these alignment effects only occur at temperatures below a certain critical temperature, called the Curie temperature (for ferromagnets and ferrimagnets) or the Néel temperature (for antiferromagnets).
Among the first investigations of ferromagnetism are the pioneering works of Aleksandr Stoletov on measurement of the magnetic permeability of ferromagnetics, known as the Stoletov curve.
Ferromagnetic materials
| Material | Curietemp. (K) |
|---|---|
| Co | 1388 |
| Fe | 1043 |
| FeOFe2O3* | 858 |
| NiOFe2O3* | 858 |
| CuOFe2O3* | 728 |
| MgOFe2O3* | 713 |
| MnBi | 630 |
| Ni | 627 |
| MnSb | 587 |
| MnOFe2O3* | 573 |
| Y3Fe5O12* | 560 |
| CrO2 | 386 |
| MnAs | 318 |
| Gd | 292 |
| Dy | 88 |
| EuO | 69 |
There are a number of crystalline materials that exhibit ferromagnetism (or ferrimagnetism). The table on the right lists a representative selection of them, along with their Curie temperatures, the temperature above which they cease to exhibit spontaneous magnetization (see below).
Ferromagnetism is a property not just of the chemical make-up of a material, but of its crystalline structure and microscopic organization. There are ferromagnetic metal alloys whose constituents are not themselves ferromagnetic, called Heusler alloys, named after Fritz Heusler. Conversely there are non-magnetic alloys, such as types of stainless steel, composed almost exclusively of ferromagnetic metals.
One can also make amorphous (non-crystalline) ferromagnetic metallic alloys by very rapid quenching (cooling) of a liquid alloy. These have the advantage that their properties are nearly isotropic (not aligned along a crystal axis); this results in low coercivity, low hysteresis loss, high permeability, and high electrical resistivity. A typical such material is a transition metal-metalloid alloy, made from about 80% transition metal (usually Fe, Co, or Ni) and a metalloid component (B, C, Si, P, or Al) that lowers the melting point.
A relatively new class of exceptionally strong ferromagnetic materials are the rare-earth magnets. They contain lanthanide elements that are known for their ability to carry large magnetic moments in well-localized f-orbitals.
Actinide ferromagnets
A number of actinide compounds are ferromagnets at room temperature or become ferromagnets below the Curie temperature (TC). PuP is one actinide pnictide that is a paramagnet and has cubic symmetry at room temperature, but upon cooling undergoes a lattice distortion to tetragonal when cooled to below its Tc = 125 K. PuP has an easy axis of <100>,[3] so that
at 5 K.[4] The lattice distortion is presumably a consequence of strain induced by the magnetoelastic interactions as the magnetic moments aligned parallel within magnetic domains.
In NpFe2 the easy axis is <111>.[5] Above TC ~500 K NpFe2 is also paramagnetic and cubic. Cooling below the Curie temperature produces a rhombohedral distortion wherein the rhombohedral angle changes from 60° (cubic phase) to 60.53°. An alternate description of this distortion is to consider the length c along the unique trigonal axis (after the distortion has begun) and a as the distance in the plane perpendicular to c. In the cubic phase this reduces to 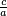 = 1.00. Below the Curie temperature
= 1.00. Below the Curie temperature
which is the largest strain in any actinide compound.[4] NpNi2 undergoes a similar lattice distortion below TC = 32 K, with a strain of (43 ± 5) × 10−4.[4] NpCo2 is a ferrimagnet below 15 K.
Lithium gas
In 2009, a team of MIT physicists demonstrated that a lithium gas cooled to less than one Kelvin can exhibit ferromagnetism.[6] The team cooled fermionic lithium-6 to less than 150 billionths of one Kelvin above absolute zero using infrared laser cooling. This demonstration is the first time that ferromagnetism has been demonstrated in a gas.
Explanation
The Bohr–van Leeuwen theorem shows that magnetism cannot occur in purely classical solids. Without quantum mechanics, there would be no diamagnetism, paramagnetism or ferromagnetism. The property of ferromagnetism is due to the direct influence of two effects from quantum mechanics: spin and the Pauli exclusion principle.[7]
Origin of magnetism
The spin of an electron, combined with its electric charge, results in a magnetic dipole moment and creates a small magnetic field. Although an electron can be visualized classically as a spinning ball of charge, spin is actually a quantum mechanical property with differences from the classical picture, such as the fact that it is quantized into discrete up/down states. The spin of the electrons in atoms is the main source of ferromagnetism, although there is also some contribution from the orbital angular momentum of the electron about the nucleus, whose classical analogue is a current loop. When these tiny magnetic dipoles are aligned in the same direction, their individual magnetic fields add together to create a measurable macroscopic field.
However in many materials (specifically, those with a filled electron shell), the total dipole moment of all the electrons is zero because the spins are in up/down pairs. Only atoms with partially filled shells (i.e., unpaired spins) can have a net magnetic moment, so ferromagnetism only occurs in materials with partially filled shells. Because of Hund’s rules, the first few electrons in a shell tend to have the same spin, thereby increasing the total dipole moment.
These unpaired dipoles (often called simply “spins” even though they also generally include angular momentum) tend to align in parallel to an external magnetic field, an effect called paramagnetism. Ferromagnetism involves an additional phenomenon, however: the dipoles tend to align spontaneously, without any applied field.
Exchange interaction
According to classical electromagnetism, two nearby magnetic dipoles will tend to align in opposite directions, so their magnetic fields will oppose one another and cancel out. However, this effect is very weak, because the magnetic fields generated by individual spins are small and the resulting alignment is easily destroyed by fluctuations. A much stronger interaction between spins arises because the change in the direction of the spin leads to a change in electrostatic repulsion between neighboring electrons, due to a particular quantum mechanical effect called exchange interaction. The electrostatic interaction energy is much stronger than the dipole-dipole magnetic interaction energy. As a result, in a few materials, the ferromagnetic ones, the spins tend to align in the same direction. The exchange interactions is related to the Pauli exclusion principle, which says that two electrons with the same spin cannot also have the same “position”. Therefore, under certain conditions, when the orbitals of the unpaired outer valence electrons from adjacent atoms overlap, the distribution of their electric charge in space is further apart when the electrons have parallel spins than when they have opposite spins. This reduces the electrostatic energy of the electrons when their spins are parallel compared to their energy when the spins are anti-parallel, so the parallel-spin state is more stable. In simple terms, the electrons, which repel one another, can move “further apart” by aligning their spins, so the spins of these electrons tend to line up. This difference in energy is called the exchange energy.
The materials in which the magnetic exchange is much stronger than the competing dipole-dipole interaction are frequently called magnetic materials. For instance, in iron (Fe) the exchange is about 1000 times stronger than the dipole interaction. Therefore below the Curie temperature virtually all of the dipoles in a ferromagnetic material will be aligned. The exchange interaction is also responsible for the other types of spontaneous ordering of atomic magnetic moments occurring in magnetic solids, antiferromagnetism and ferrimagnetism. Depending on the material’s chemistry, different specific mechanisms of magnetic exchange become important. These mechanisms include direct exchange, RKKY exchange, double exchange, superexchange, and so on, and may each favor both ferro- and antiferromagnetic allignment, depending on various factors.
Magnetic anisotropy
Although the exchange interaction keeps spins aligned, it does not align them in any particular direction. Without magnetic anisotropy, the spins in a magnet randomly change direction in response to thermal fluctuations and the magnet is superparamagnetic. There are several kinds of magnetic anisotropy, the most common of which is magnetocrystalline anisotropy. This is a dependence of the energy on the direction of magnetization relative to the crystallographic lattice. Another common source of anisotropy, inverse magnetostriction, is induced by internal strains. Single-domain magnets also can have a shape anisotropy due to the magnetostatic effects of the particle shape. As the temperature of a magnet increases, the anisotropy tends to decrease, and there is often a blocking temperature at which a transition to superparamagnetism occurs.[8]
Magnetic domains
The above would seem to suggest that every piece of ferromagnetic material should have a strong magnetic field, since all the spins are aligned, yet iron and other ferromagnets are often found in an “unmagnetized” state.
The reason for this is that a bulk piece of ferromagnetic material is divided into many tiny magnetic domains (also known as Weiss domains). Within each domain, the spins are aligned, but (if the bulk material is in its lowest energy configuration, i.e. “unmagnetized”), the spins of separate domains point in different directions and their magnetic fields cancel out, so the object has no net large scale magnetic field.
Ferromagnetic materials spontaneously divide into magnetic domains because this is a lower energy configuration. At long distances (after many thousands of ions), the exchange energy advantage is overtaken by the classical tendency of dipoles to anti-align. The boundary between two domains, where the magnetization flips, is called a domain wall (i.e., a Bloch/Néel wall, depending upon whether the magnetization rotates parallel/perpendicular to the domain interface) and is a gradual transition on the atomic scale (covering a distance of about 300 ions for iron).
Thus, an ordinary piece of iron generally has little or no net magnetic moment. However, if it is placed in a strong enough external magnetic field, the domains will re-orient in parallel with that field, and will remain re-oriented when the field is turned off, thus creating a “permanent” magnet. The domains don’t go back to their original minimum energy configuration when the field is turned off because the domain walls tend to become ‘pinned’ or ‘snagged’ on defects in the crystal lattice, preserving their parallel orientation. This is shown by the Barkhausen effect: as the magnetizing field is changed, the magnetization changes in thousands of tiny discontinuous jumps as the domain walls suddenly “snap” past defects.
This magnetization as a function of the external field is described by a hysteresis curve. Although this state of aligned domains is not a minimal-energy configuration, it is extremely stable and has been observed to persist for millions of years in seafloor magnetite aligned by the Earth’s magnetic field (whose poles can thereby be seen to flip at long intervals).
Alloys used for the strongest permanent magnets are “hard” alloys made with many defects in their crystal structure where the domain walls “catch” and stabilize. The net magnetization can be destroyed by heating and then cooling (annealing) the material without an external field, however. The thermal motion allows the domain boundaries to move, releasing them from any defects, to return to their low-energy unaligned state.
Curie temperature
As the temperature increases, thermal motion, or entropy, competes with the ferromagnetic tendency for dipoles to align. When the temperature rises beyond a certain point, called the Curie temperature, there is a second-order phase transition and the system can no longer maintain a spontaneous magnetization, although it still responds paramagnetically to an external field. Below that temperature, there is a spontaneous symmetry breaking and random domains form (in the absence of an external field). The Curie temperature itself is a critical point, where the magnetic susceptibility is theoretically infinite and, although there is no net magnetization, domain-like spin correlations fluctuate at all length scales.
The study of ferromagnetic phase transitions, especially via the simplified Ising spin model, had an important impact on the development of statistical physics. There, it was first clearly shown that mean field theory approaches failed to predict the correct behavior at the critical point (which was found to fall under a universality class that includes many other systems, such as liquid-gas transitions), and had to be replaced by renormalization group theory.
See also
References
- ^ Richard M. Bozorth, Ferromagnetism, first published 1951, reprinted 1993 by IEEE Press, New York as a “Classic Reissue.” ISBN 0-7803-1032-2.
- ^ Kittel, Charles (1986). Introduction to Solid State Physics (sixth ed.). John Wiley and Sons. ISBN 0-471-87474-4.
- ^ Lander GH, Lam DJ (1976). “Neutron diffraction study of PuP: The electronic ground state”. Phys Rev B. 14 (9): 4064–7. Bibcode 1976PhRvB..14.4064L. doi:10.1103/PhysRevB.14.4064.
- ^ a b c Mueller MH, Lander GH, Hoff HA, Knott HW, Reddy JF (Apr 1979). “Lattice distortions measured in actinide ferromagnets PuP, NpFe2, and NpNi2“. J Phys Colloque C4, supplement 40 (4): C4–68–C4–69. http://hal.archives-ouvertes.fr/docs/00/21/88/17/PDF/ajp-jphyscol197940C421.pdf.
- ^ Aldred AT, Dunlap BD, Lam DJ, Lander GH, Mueller MH, Nowik I (1975). “Magnetic properties of neptunium Laves phases: NpMn2, NpFe2, NpCo2, and NpNi2“. Phys Rev B. 11 (1): 530–44. Bibcode 1975PhRvB..11..530A. doi:10.1103/PhysRevB.11.530.
- ^ G-B Jo, Y-R Lee, J-H Choi, C. A. Christensen, T. H. Kim, J. H. Thywissen, D. E. Pritchard, and W. Ketterle (2009). “Itinerant Ferromagnetism in a Fermi Gas of Ultracold Atoms”. Science 325 (5947): 1521–1524. Bibcode 2009Sci…325.1521J. doi:10.1126/science.1177112. PMID 19762638.
- ^ Feynman, Richard P.; Robert Leighton, Matthew Sands (1963). The Feynman Lectures on Physics, Vol.2. USA: Addison-Wesley. pp. Ch. 37. ISBN 0201020114H.
- ^ Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. ISBN 0198517912. http://www.oup.com/us/catalog/general/subject/Physics/ElectricityMagnetism/?view=usa&ci=9780198508090.
Bibliography
- Charles Kittel, Introduction to Solid State Physics (Wiley: New York, 1996).
- Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
- John David Jackson, Classical Electrodynamics (Wiley: New York, 1999).
- E. P. Wohlfarth, ed., Ferromagnetic Materials (North-Holland, 1980).
- “Heusler alloy,” Encyclopædia Britannica Online, retrieved Jan. 23, 2005.
- F. Heusler, W. Stark, and E. Haupt, Verh. der Phys. Ges. 5, 219 (1903).
- S. Vonsovsky Magnetism of elementary particles (Mir Publishers, Moscow, 1975).
- Tyablikov S. V. (1995): Methods in the Quantum Theory of Magnetism. Springer; 1st edition. ISBN 0-306-30263-2.
External links
- Electromagnetism – a chapter from an online textbook
- Sandeman, Karl (January 2008). “Ferromagnetic Materials”. DoITPoMS. Dept. of Materials Sci. and Metallurgy, Univ. of Cambridge. http://www.msm.cam.ac.uk/doitpoms/tlplib/ferromagnetic/printall.php. Retrieved 2008-08-27. Detailed nonmathematical description of ferromagnetic materials with animated illustrations
|
|||||
This information originally retrieved from http://en.wikipedia.org/wiki/Ferromagnetism
on Wednesday 3rd August 2011 9:53 pm EDT
Now edited and maintained by ManufacturingET.org