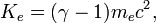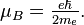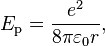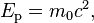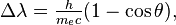and a negative electric charge of 1 elementary charge. It has no known components or substructure. Therefore, the electron is generally thought to be an elementary particle.[2] An electron has a mass that is approximately 1/1836 that of the proton[8]. The intrinsic angular momentum (spin) of the electron is a half-integer value in units of ħ, which means that it is a fermion. The antiparticle of the electron is called the positron. The positron is identical to the electron except that it carries electrical and other charges of the opposite sign. When an electron collides with a positron, both particles may either scatter off each other or be totally annihilated, producing a pair (or more) of gamma ray photons. Electrons, which belong to the first generation of the lepton particle family,[9] participate in gravitational, electromagnetic and weak interactions.[10] Electrons, like all matter, have quantum mechanical properties of both particles and waves, so they can collide with other particles and be diffracted like light. However, this duality is best demonstrated in experiments with electrons, due to their tiny mass. Since an electron is a fermion, no two electrons can occupy the same quantum state, in accordance with the Pauli exclusion principle.[9]
The concept of an indivisible quantity of electric charge was theorized to explain the chemical properties of atoms, beginning in 1838 by British natural philosopher Richard Laming;[4] the name electron was introduced for this charge in 1894 by Irish physicist George Johnstone Stoney. The electron was identified as a particle in 1897 by J. J. Thomson and his team of British physicists.[6][11][12]
In many physical phenomena, such as electricity, magnetism, and thermal conductivity, electrons play an essential role. An electron in motion relative to an observer generates a magnetic field, and will be deflected by external magnetic fields. When an electron is accelerated, it can absorb or radiate energy in the form of photons. Electrons, together with atomic nuclei made of protons and neutrons, make up atoms. However, electrons contribute less than 0.06% to an atom’s total mass. The attractive Coulomb force between an electron and a proton causes electrons to be bound into atoms. The exchange or sharing of the electrons between two or more atoms is the main cause of chemical bonding.[13]
According to theory, most electrons in the universe were created in the big bang, but they may also be created through beta decay of radioactive isotopes and in high-energy collisions, for instance when cosmic rays enter the atmosphere. Electrons may be destroyed through annihilation with positrons, and may be absorbed during nucleosynthesis in stars. Laboratory instruments are capable of containing and observing individual electrons as well as electron plasma, whereas dedicated telescopes can detect electron plasma in outer space. Electrons have many applications, including welding, cathode ray tubes, electron microscopes, radiation therapy, lasers and particle accelerators.
Contents |
History
The ancient Greeks noticed that amber attracted small objects when rubbed with fur. Apart from lightning, this phenomenon is humanity’s earliest recorded experience with electricity.[14] In his 1600 treatise De Magnete, the English scientist William Gilbert coined the New Latin term electricus, to refer to this property of attracting small objects after being rubbed.[15] Both electric and electricity are derived from the Latin ēlectrum (also the root of the alloy of the same name), which came from the Greek word ήλεκτρον (ēlektron) for amber.
In 1737 C. F. du Fay and Hawksbee independently discovered what they believed to be two kinds of frictional electricity; one generated from rubbing glass, the other from rubbing resin. From this, Du Fay theorized that electricity consists of two electrical fluids, “vitreous” and “resinous”, that are separated by friction and that neutralize each other when combined.[16] A decade later Benjamin Franklin proposed that electricity was not from different types of electrical fluid, but the same electrical fluid under different pressures. He gave them the modern charge nomenclature of positive and negative respectively.[17] Franklin thought that the charge carrier was positive.[18]
Between 1838 and 1851, British natural philosopher Richard Laming developed the idea that an atom is composed of a core of matter surrounded by subatomic particles that had unit electric charges.[3] Beginning in 1846, German physicist William Weber theorized that electricity was composed of positively and negatively charged fluids, and their interaction was governed by the inverse square law. After studying the phenomenon of electrolysis in 1874, Irish physicist George Johnstone Stoney suggested that there existed a “single definite quantity of electricity”, the charge of a monovalent ion. He was able to estimate the value of this elementary charge e by means of Faraday’s laws of electrolysis.[19] However, Stoney believed these charges were permanently attached to atoms and could not be removed. In 1881, German physicist Hermann von Helmholtz argued that both positive and negative charges were divided into elementary parts, each of which “behaves like atoms of electricity”.[4]
In 1894, Stoney coined the term electron to describe these elementary charges, saying, “… an estimate was made of the actual amount of this most remarkable fundamental unit of electricity, for which I have since ventured to suggest the name electron“.[20] The word electron is a combination of the word electric and the suffix –on, with the latter now used to designate a subatomic particle, such as a proton or neutron.[21][22]
Discovery
A beam of electrons deflected in a circle by a magnetic field[23]
The German physicist Johann Wilhelm Hittorf undertook the study of electrical conductivity in rarefied gases. In 1869, he discovered a glow emitted from the cathode that increased in size with decrease in gas pressure. In 1876, the German physicist Eugen Goldstein showed that the rays from this glow cast a shadow, and he dubbed the rays cathode rays.[24] During the 1870s, the English chemist and physicist Sir William Crookes developed the first cathode ray tube to have a high vacuum inside.[25] He then showed that the luminescence rays appearing within the tube carried energy and moved from the cathode to the anode. Furthermore, by applying a magnetic field, he was able to deflect the rays, thereby demonstrating that the beam behaved as though it were negatively charged.[26][27] In 1879, he proposed that these properties could be explained by what he termed ‘radiant matter’. He suggested that this was a fourth state of matter, consisting of negatively charged molecules that were being projected with high velocity from the cathode.[28]
The German-born British physicist Arthur Schuster expanded upon Crookes’ experiments by placing metal plates parallel to the cathode rays and applying an electric potential between the plates. The field deflected the rays toward the positively charged plate, providing further evidence that the rays carried negative charge. By measuring the amount of deflection for a given level of current, in 1890 Schuster was able to estimate the charge-to-mass ratio of the ray components. However, this produced a value that was more than a thousand times greater than what was expected, so little credence was given to his calculations at the time.[26][29]
In 1896, the British physicist J. J. Thomson, with his colleagues John S. Townsend and H. A. Wilson,[11] performed experiments indicating that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier.[6] Thomson made good estimates of both the charge e and the mass m, finding that cathode ray particles, which he called “corpuscles,” had perhaps one thousandth of the mass of the least massive ion known: hydrogen.[6][12] He showed that their charge to mass ratio, e/m, was independent of cathode material. He further showed that the negatively charged particles produced by radioactive materials, by heated materials and by illuminated materials were universal.[6][30] The name electron was again proposed for these particles by the Irish physicist George F. Fitzgerald, and the name has since gained universal acceptance.[26]
While studying naturally fluorescing minerals in 1896, the French physicist Henri Becquerel discovered that they emitted radiation without any exposure to an external energy source. These radioactive materials became the subject of much interest by scientists, including the New Zealand physicist Ernest Rutherford who discovered they emitted particles. He designated these particles alpha and beta, on the basis of their ability to penetrate matter.[31] In 1900, Becquerel showed that the beta rays emitted by radium could be deflected by an electric field, and that their mass-to-charge ratio was the same as for cathode rays.[32] This evidence strengthened the view that electrons existed as components of atoms.[33][34]
The electron’s charge was more carefully measured by the American physicist Robert Millikan in his oil-drop experiment of 1909, the results of which he published in 1911. This experiment used an electric field to prevent a charged droplet of oil from falling as a result of gravity. This device could measure the electric charge from as few as 1–150 ions with an error margin of less than 0.3%. Comparable experiments had been done earlier by Thomson’s team,[6] using clouds of charged water droplets generated by electrolysis,[11] and in 1911 by Abram Ioffe, who independently obtained the same result as Millikan using charged microparticles of metals, then published his results in 1913.[35] However, oil drops were more stable than water drops because of their slower evaporation rate, and thus more suited to precise experimentation over longer periods of time.[36]
Around the beginning of the twentieth century, it was found that under certain conditions a fast moving charged particle caused a condensation of supersaturated water vapor along its path. In 1911, Charles Wilson used this principle to devise his cloud chamber, allowing the tracks of charged particles, such as fast-moving electrons, to be photographed.[37]
Atomic theory
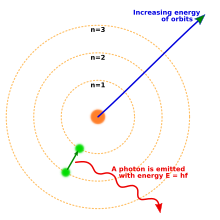
The Bohr model of the atom, showing states of electron with energy quantized by the number n. An electron dropping to a lower orbit emits a photon equal to the energy difference between the orbits.
By 1914, experiments by physicists Ernest Rutherford, Henry Moseley, James Franck and Gustav Hertz had largely established the structure of an atom as a dense nucleus of positive charge surrounded by lower-mass electrons.[38] In 1913, Danish physicist Niels Bohr postulated that electrons resided in quantized energy states, with the energy determined by the angular momentum of the electron’s orbits about the nucleus. The electrons could move between these states, or orbits, by the emission or absorption of photons at specific frequencies. By means of these quantized orbits, he accurately explained the spectral lines of the hydrogen atom.[39] However, Bohr’s model failed to account for the relative intensities of the spectral lines and it was unsuccessful in explaining the spectra of more complex atoms.[38]
Chemical bonds between atoms were explained by Gilbert Newton Lewis, who in 1916 proposed that a covalent bond between two atoms is maintained by a pair of electrons shared between them.[40] Later, in 1923, Walter Heitler and Fritz London gave the full explanation of the electron-pair formation and chemical bonding in terms of quantum mechanics.[41] In 1919, the American chemist Irving Langmuir elaborated on the Lewis’ static model of the atom and suggested that all electrons were distributed in successive “concentric (nearly) spherical shells, all of equal thickness”.[42] The shells were, in turn, divided by him in a number of cells each containing one pair of electrons. With this model Langmuir was able to qualitatively explain the chemical properties of all elements in the periodic table,[41] which were known to largely repeat themselves according to the periodic law.[43]
In 1924, Austrian physicist Wolfgang Pauli observed that the shell-like structure of the atom could be explained by a set of four parameters that defined every quantum energy state, as long as each state was inhabited by no more than a single electron. (This prohibition against more than one electron occupying the same quantum energy state became known as the Pauli exclusion principle.)[44] The physical mechanism to explain the fourth parameter, which had two distinct possible values, was provided by the Dutch physicists Abraham Goudsmith and George Uhlenbeck when they suggested that an electron, in addition to the angular momentum of its orbit, could possess an intrinsic angular momentum.[38][45] This property became known as spin, and explained the previously mysterious splitting of spectral lines observed with a high-resolution spectrograph; this phenomenon is known as fine structure splitting.[46]
Quantum mechanics
In his 1924 dissertation Recherches sur la théorie des quanta (Research on Quantum Theory), French physicist Louis de Broglie hypothesized that all matter possesses a De Broglie wave similar to light.[47] That is, under the appropriate conditions, electrons and other matter would show properties of either particles or waves. The corpuscular properties of a particle are demonstrated when it is shown to have a localized position in space along its trajectory at any given moment.[48] Wave-like nature is observed, for example, when a beam of light is passed through parallel slits and creates interference patterns. In 1927, the interference effect was demonstrated with a beam of electrons by English physicist George Paget Thomson with a thin metal film and by American physicists Clinton Davisson and Lester Germer using a crystal of nickel.[49]
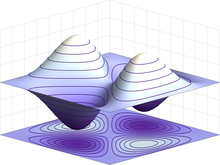
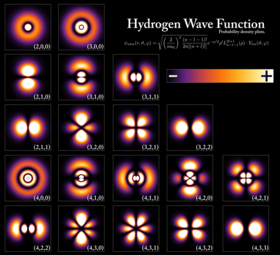
In quantum mechanics, the behavior of an electron in an atom is described by an orbital, which is a probability distribution rather than an orbit. In the figure, the shading indicates the relative probability to “find” the electron, having the energy corresponding to the given quantum numbers, at that point.
The success of de Broglie’s prediction led to the publication, by Erwin Schrödinger in 1926, of the Schrödinger equation that successfully describes how electron waves propagated.[50] Rather than yielding a solution that determines the location of an electron over time, this wave equation can be used to predict the probability of finding an electron near a position. This approach was later called quantum mechanics, which provided an extremely close derivation to the energy states of an electron in a hydrogen atom.[51] Once spin and the interaction between multiple electrons were considered, quantum mechanics allowed the configuration of electrons in atoms with higher atomic numbers than hydrogen to be successfully predicted.[52]
In 1928, building on Wolfgang Pauli’s work, Paul Dirac produced a model of the electron – the Dirac equation, consistent with relativity theory, by applying relativistic and symmetry considerations to the hamiltonian formulation of the quantum mechanics of the electro-magnetic field.[53] In order to resolve some problems within his relativistic equation, in 1930 Dirac developed a model of the vacuum as an infinite sea of particles having negative energy, which was dubbed the Dirac sea. This led him to predict the existence of a positron, the antimatter counterpart of the electron.[54] This particle was discovered in 1932 by Carl D. Anderson, who proposed calling standard electrons negatrons, and using electron as a generic term to describe both the positively and negatively charged variants. This usage of the term ‘negatron’ is still occasionally encountered today, and it may be shortened to ‘negaton’.[55][56]
In 1947 Willis Lamb, working in collaboration with graduate student Robert Rutherford, found that certain quantum states of hydrogen atom, which should have the same energy, were shifted in relation to each other, the difference being the Lamb shift. About the same time, Polykarp Kusch, working with Henry M. Foley, discovered the magnetic moment of the electron is slightly larger than predicted by Dirac’s theory. This small difference was later called anomalous magnetic dipole moment of the electron. To resolve these issues, a refined theory called quantum electrodynamics was developed by Sin-Itiro Tomonaga, Julian Schwinger and Richard P. Feynman in the late 1940s.[57]
Particle accelerators
With the development of the particle accelerator during the first half of the twentieth century, physicists began to delve deeper into the properties of subatomic particles.[58] The first successful attempt to accelerate electrons using electromagnetic induction was made in 1942 by Donald Kerst. His initial betatron reached energies of 2.3 MeV, while subsequent betatrons achieved 300 MeV. In 1947, synchrotron radiation was discovered with a 70 MeV electron synchrotron at General Electric. This radiation was caused by the acceleration of electrons, moving near the speed of light, through a magnetic field.[59]
With a beam energy of 1.5 GeV, the first high-energy particle collider was ADONE, which began operations in 1968.[60] This device accelerated electrons and positrons in opposite directions, effectively doubling the energy of their collision when compared to striking a static target with an electron.[61] The Large Electron-Positron Collider (LEP) at CERN, which was operational from 1989 to 2000, achieved collision energies of 209 GeV and made important measurements for the Standard Model of particle physics.[62][63]
Characteristics
Classification
In the Standard Model of particle physics, electrons belong to the group of subatomic particles called leptons, which are believed to be fundamental or elementary particles. Electrons have the lowest mass of any charged lepton (or electrically charged particle of any type) and belong to the first-generation of fundamental particles.[64] The second and third generation contain charged leptons, the muon and the tau, which are identical to the electron in charge, spin and interactions, but are more massive. Leptons differ from the other basic constituent of matter, the quarks, by their lack of strong interaction. All members of the lepton group are fermions, because they all have half-odd integer spin; the electron has spin 1⁄2.[65]
Fundamental properties
The invariant mass of an electron is approximately 9.109×10−31 kilogram,[66] or 5.489×10−4 atomic mass unit. On the basis of Einstein‘s principle of mass–energy equivalence, this mass corresponds to a rest energy of 0.511 MeV. The ratio between the mass of a proton and that of an electron is about 1836.[8][67] Astronomical measurements show that the proton-to-electron mass ratio has held the same value for at least half the age of the universe, as is predicted by the Standard Model.[68]
Electrons have an electric charge of −1.602×10−19 coulomb,[66] which is used as a standard unit of charge for subatomic particles. Within the limits of experimental accuracy, the electron charge is identical to the charge of a proton, but with the opposite sign.[69] As the symbol e is used for the elementary charge, the electron is commonly symbolized by e−
, where the minus sign indicates the negative charge. The positron is symbolized by e+
because it has the same properties as the electron but with a positive rather than negative charge.[66][65]
The electron has an intrinsic angular momentum or spin of 1⁄2.[66] This property is usually stated by referring to the electron as a spin-1⁄2 particle.[65] For such particles the spin magnitude is √3⁄2 ħ.[note 3] while the result of the measurement of a projection of the spin on any axis can only be ±ħ⁄2. In addition to spin, the electron has an intrinsic magnetic moment along its spin axis.[66] It is approximately equal to one Bohr magneton,[70][note 4] which is a physical constant equal to 9.27400915(23)×10−24 joules per tesla.[66] The orientation of the spin with respect to the momentum of the electron defines the property of elementary particles known as helicity.[71]
The electron has no known substructure.[2][72] Hence, it is defined or assumed to be a point particle with a point charge and no spatial extent.[9] Observation of a single electron in a Penning trap shows the upper limit of the particle’s radius is 10−22 meters.[73] There is a physical constant called the “classical electron radius“, with the much larger value of 2.8179×10−15 m. However, the terminology comes from a simplistic calculation that ignores the effects of quantum mechanics; in reality, the so-called classical electron radius has little to do with the true fundamental structure of the electron.[74][note 5]
There are elementary particles that spontaneously decay into less massive particles. An example is the muon, which decays into an electron, a neutrino and an antineutrino, with a mean lifetime of 2.2×10−6 seconds. However, the electron is thought to be stable on theoretical grounds: the electron is the least massive particle with non-zero electric charge, so its decay would violate charge conservation.[75] The experimental lower bound for the electron’s mean lifetime is 4.6×1026 years, at a 90% confidence level.[76]
Quantum properties
As with all particles, electrons can act as waves. This is called the wave–particle duality and can be demonstrated using the double-slit experiment. The wave-like nature of the electron allows it to pass through two parallel slits simultaneously, rather than just one slit as would be the case for a classical particle. In quantum mechanics, the wave-like property of one particle can be described mathematically as a complex-valued function, the wave function, commonly denoted by the Greek letter psi (ψ). When the absolute value of this function is squared, it gives the probability that a particle will be observed near a location—a probability density.[77]
Example of an antisymmetric wave function for a quantum state of two identical fermions in a 1-dimensional box. If the particles swap position, the wave function inverts its sign.
Electrons are identical particles because they cannot be distinguished from each other by their intrinsic physical properties. In quantum mechanics, this means that a pair of interacting electrons must be able to swap positions without an observable change to the state of the system. The wave function of fermions, including electrons, is antisymmetric, meaning that it changes sign when two electrons are swapped; that is, ψ(r1, r2) = −ψ(r2, r1), where the variables r1 and r2 correspond to the first and second electrons, respectively. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. Bosons, such as the photon, have symmetric wave functions instead.[77]
In the case of antisymmetry, solutions of the wave equation for interacting electrons result in a zero probability that each pair will occupy the same location or state. This is responsible for the Pauli exclusion principle, which precludes any two electrons from occupying the same quantum state. This principle explains many of the properties of electrons. For example, it causes groups of bound electrons to occupy different orbitals in an atom, rather than all overlapping each other in the same orbit.[77]
Virtual particles
Physicists believe that empty space may be continually creating pairs of virtual particles, such as a positron and electron, which rapidly annihilate each other shortly thereafter.[78] The combination of the energy variation needed to create these particles, and the time during which they exist, fall under the threshold of detectability expressed by the Heisenberg uncertainty relation, ΔE · Δt ≥ ħ. In effect, the energy needed to create these virtual particles, ΔE, can be “borrowed” from the vacuum for a period of time, Δt, so that their product is no more than the reduced Planck constant, ħ ≈ 6.6×10−16 eV·s. Thus, for a virtual electron, Δt is at most 1.3×10−21 s.[79]
While an electron–positron virtual pair is in existence, the coulomb force from the ambient electric field surrounding an electron causes a created positron to be attracted to the original electron, while a created electron experiences a repulsion. This causes what is called vacuum polarization. In effect, the vacuum behaves like a medium having a dielectric permittivity more than unity. Thus the effective charge of an electron is actually smaller than its true value, and the charge decreases with increasing distance from the electron.[80][81] This polarization was confirmed experimentally in 1997 using the Japanese TRISTAN particle accelerator.[82] Virtual particles cause a comparable shielding effect for the mass of the electron.[83]
The interaction with virtual particles also explains the small (about 0.1%) deviation of the intrinsic magnetic moment of the electron from the Bohr magneton (the anomalous magnetic moment).[70][84] The extraordinarily precise agreement of this predicted difference with the experimentally determined value is viewed as one of the great achievements of quantum electrodynamics.[85]
In classical physics, the angular momentum and magnetic moment of an object depend upon its physical dimensions. Hence, the concept of a dimensionless electron possessing these properties might seem inconsistent. The apparent paradox can be explained by the formation of virtual photons in the electric field generated by the electron. These photons cause the electron to shift about in a jittery fashion (known as zitterbewegung),[86] which results in a net circular motion with precession. This motion produces both the spin and the magnetic moment of the electron.[9][87] In atoms, this creation of virtual photons explains the Lamb shift observed in spectral lines.[80]
Interaction
An electron generates an electric field that exerts an attractive force on a particle with a positive charge, such as the proton, and a repulsive force on a particle with a negative charge. The strength of this force is determined by Coulomb’s inverse square law.[88] When an electron is in motion, it generates a magnetic field.[89] The Ampère-Maxwell law relates the magnetic field to the mass motion of electrons (the current) with respect to an observer. It is this property of induction which supplies the magnetic field that drives an electric motor.[90] The electromagnetic field of an arbitrary moving charged particle is expressed by the Liénard–Wiechert potentials, which are valid even when the particle’s speed is close to that of light (relativistic).
When an electron is moving through a magnetic field, it is subject to the Lorentz force that exerts an influence in a direction perpendicular to the plane defined by the magnetic field and the electron velocity. This centripetal force causes the electron to follow a helical trajectory through the field at a radius called the gyroradius. The acceleration from this curving motion induces the electron to radiate energy in the form of synchrotron radiation.[91][92][note 6] The energy emission in turn causes a recoil of the electron, known as the Abraham-Lorentz-Dirac force, which creates a friction that slows the electron. This force is caused by a back-reaction of the electron’s own field upon itself.[93]
In quantum electrodynamics the electromagnetic interaction between particles is mediated by photons. An isolated electron that is not undergoing acceleration is unable to emit or absorb a real photon; doing so would violate conservation of energy and momentum. Instead, virtual photons can transfer momentum between two charged particles. It is this exchange of virtual photons that, for example, generates the Coulomb force.[94] Energy emission can occur when a moving electron is deflected by a charged particle, such as a proton. The acceleration of the electron results in the emission of Bremsstrahlung radiation.[95]
An inelastic collision between a photon (light) and a solitary (free) electron is called Compton scattering. This collision results in a transfer of momentum and energy between the particles, which modifies the wavelength of the photon by an amount called the Compton shift.[note 7] The maximum magnitude of this wavelength shift is h/mec, which is known as the Compton wavelength.[96] For an electron, it has a value of 2.43×10−12 m.[66] When the wavelength of the light is long (for instance, the wavelength of the visible light is 0.4–0.7 μm) the wavelength shift becomes negligible. Such interaction between the light and free electrons is called Thomson scattering or Linear Thomson scattering.[97]
The relative strength of the electromagnetic interaction between two charged particles, such as an electron and a proton, is given by the fine-structure constant. This value is a dimensionless quantity formed by the ratio of two energies: the electrostatic energy of attraction (or repulsion) at a separation of one Compton wavelength, and the rest energy of the charge. It is given by α ≈ 7.297353×10−3, which is approximately equal to 1⁄137.[66]
When electrons and positrons collide, they annihilate each other, giving rise to two or more gamma ray photons. If the electron and positron have negligible momentum, a positronium atom can form before annihilation results in two or three gamma ray photons totalling 1.022 MeV.[98][99] On the other hand, high-energy photons may transform into an electron and a positron by a process called pair production, but only in the presence of a nearby charged particle, such as a nucleus.[100][101]
In the theory of electroweak interaction, the left-handed component of electron’s wavefunction forms a weak isospin doublet with the electron neutrino. This means that during weak interactions, electron neutrinos behave like electrons. Either member of this doublet can undergo a charged current interaction by emitting or absorbing a W and be converted into the other member. Charge is conserved during this reaction because the W boson also carries a charge, canceling out any net change during the transmutation. Charged current interactions are responsible for the phenomenon of beta decay in a radioactive atom. Both the electron and electron neutrino can undergo a neutral current interaction via a Z0
exchange, and this is responsible for neutrino-electron elastic scattering.[102]
Atoms and molecules
An electron can be bound to the nucleus of an atom by the attractive Coulomb force. A system of several electrons bound to a nucleus is called an atom. If the number of electrons is different from the nucleus’ electrical charge, such an atom is called an ion. The wave-like behavior of a bound electron is described by a function called an atomic orbital. Each orbital has its own set of quantum numbers such as energy, angular momentum and projection of angular momentum, and only a discrete set of these orbitals exist around the nucleus. According to the Pauli exclusion principal each orbital can be occupied by up to two electrons, which must differ in their spin quantum number.
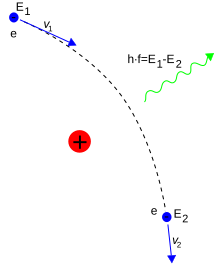
Electrons can transfer between different orbitals by the emission or absorption of photons with an energy that matches the difference in potential.[103] Other methods of orbital transfer include collisions with particles, such as electrons, and the Auger effect.[104] In order to escape the atom, the energy of the electron must be increased above its binding energy to the atom. This occurs, for example, with the photoelectric effect, where an incident photon exceeding the atom’s ionization energy is absorbed by the electron.[105]
The orbital angular momentum of electrons is quantized. Because the electron is charged, it produces an orbital magnetic moment that is proportional to the angular momentum. The net magnetic moment of an atom is equal to the vector sum of orbital and spin magnetic moments of all electrons and the nucleus. The magnetic moment of the nucleus is negligible compared with that of the electrons. The magnetic moments of the electrons that occupy the same orbital (so called, paired electrons) cancel each other out.[106]
The chemical bond between atoms occurs as a result of electromagnetic interactions, as described by the laws of quantum mechanics.[107] The strongest bonds are formed by the sharing or transfer of electrons between atoms, allowing the formation of molecules.[13] Within a molecule, electrons move under the influence of several nuclei, and occupy molecular orbitals; much as they can occupy atomic orbitals in isolated atoms.[108] A fundamental factor in these molecular structures is the existence of electron pairs. These are electrons with opposed spins, allowing them to occupy the same molecular orbital without violating the Pauli exclusion principle (much like in atoms). Different molecular orbitals have different spatial distribution of the electron density. For instance, in bonded pairs (i.e. in the pairs that actually bind atoms together) electrons can be found with the maximal probability in a relatively small volume between the nuclei. On the contrary, in non-bonded pairs electrons are distributed in a large volume around nuclei.[109]
Conductivity
If a body has more or fewer electrons than are required to balance the positive charge of the nuclei, then that object has a net electric charge. When there is an excess of electrons, the object is said to be negatively charged. When there are fewer electrons than the number of protons in nuclei, the object is said to be positively charged. When the number of electrons and the number of protons are equal, their charges cancel each other and the object is said to be electrically neutral. A macroscopic body can develop an electric charge through rubbing, by the triboelectric effect.[113]
Independent electrons moving in vacuum are termed free electrons. Electrons in metals also behave as if they were free. In reality the particles that are commonly termed electrons in metals and other solids are quasi-electrons—quasi-particles, which have the same electrical charge, spin and magnetic moment as real electrons but may have a different mass.[114] When free electrons—both in vacuum and metals—move, they produce a net flow of charge called an electric current, which generates a magnetic field. Likewise a current can be created by a changing magnetic field. These interactions are described mathematically by Maxwell’s equations.[115]
At a given temperature, each material has an electrical conductivity that determines the value of electric current when an electric potential is applied. Examples of good conductors include metals such as copper and gold, whereas glass and Teflon are poor conductors. In any dielectric material, the electrons remain bound to their respective atoms and the material behaves as an insulator. Most semiconductors have a variable level of conductivity that lies between the extremes of conduction and insulation.[116] On the other hand, metals have an electronic band structure containing partially filled electronic bands. The presence of such bands allows electrons in metals to behave as if they were free or delocalized electrons. These electrons are not associated with specific atoms, so when an electric field is applied, they are free to move like a gas (called Fermi gas)[117] through the material much like free electrons.
Because of collisions between electrons and atoms, the drift velocity of electrons in a conductor is on the order of millimeters per second. However, the speed at which a change of current at one point in the material causes changes in currents in other parts of the material, the velocity of propagation, is typically about 75% of light speed.[118] This occurs because electrical signals propagate as a wave, with the velocity dependent on the dielectric constant of the material.[119]
Metals make relatively good conductors of heat, primarily because the delocalized electrons are free to transport thermal energy between atoms. However, unlike electrical conductivity, the thermal conductivity of a metal is nearly independent of temperature. This is expressed mathematically by the Wiedemann-Franz law,[117] which states that the ratio of thermal conductivity to the electrical conductivity is proportional to the temperature. The thermal disorder in the metallic lattice increases the electrical resistivity of the material, producing a temperature dependence for electrical current.[120]
When cooled below a point called the critical temperature, materials can undergo a phase transition in which they lose all resistivity to electrical current, in a process known as superconductivity. In BCS theory, this behavior is modeled by pairs of electrons entering a quantum state known as a Bose–Einstein condensate. These Cooper pairs have their motion coupled to nearby matter via lattice vibrations called phonons, thereby avoiding the collisions with atoms that normally create electrical resistance.[121] (Cooper pairs have a radius of roughly 100 nm, so they can overlap each other.)[122] However, the mechanism by which higher temperature superconductors operate remains uncertain.
Electrons inside conducting solids, which are quasi-particles themselves, when tightly confined at temperatures close to absolute zero, behave as though they had split into two other quasiparticles: spinons and holons.[123][124] The former carries spin and magnetic moment, while the latter electrical charge.
Motion and energy
According to Einstein’s theory of special relativity, as an electron’s speed approaches the speed of light, from an observer’s point of view its relativistic mass increases, thereby making it more and more difficult to accelerate it from within the observer’s frame of reference. The speed of an electron can approach, but never reach, the speed of light in a vacuum, c. However, when relativistic electrons—that is, electrons moving at a speed close to c—are injected into a dielectric medium such as water, where the local speed of light is significantly less than c, the electrons temporarily travel faster than light in the medium. As they interact with the medium, they generate a faint light called Cherenkov radiation.[125]
The effects of special relativity are based on a quantity known as the Lorentz factor, defined as 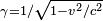 where v is the speed of the particle. The kinetic energy Ke of an electron moving with velocity v is:
where v is the speed of the particle. The kinetic energy Ke of an electron moving with velocity v is:
where me is the mass of electron. For example, the Stanford linear accelerator can accelerate an electron to roughly 51 GeV.[126] Since an electron behaves as a wave, at a given velocity it has a characteristic de Broglie wavelength. This is given by λe = h/p where h is the Planck constant and p is the momentum.[47] For the 51 GeV electron above, the wavelength is about 2.4×10−17 m, small enough to explore structures well below the size of an atomic nucleus.[127]
Formation
Pair production caused by the collision of a photon with an atomic nucleus
The Big Bang theory is the most widely accepted scientific theory to explain the early stages in the evolution of the Universe.[128] For the first millisecond of the Big Bang, the temperatures were over 10 billion kelvins and photons had mean energies over a million electronvolts. These photons were sufficiently energetic that they could react with each other to form pairs of electrons and positrons. Likewise, positron-electron pairs annihilated each other and emitted energetic photons:
An equilibrium between electrons, positrons and photons was maintained during this phase of the evolution of the Universe. After 15 seconds had passed, however, the temperature of the universe dropped below the threshold where electron-positron formation could occur. Most of the surviving electrons and positrons annihilated each other, releasing gamma radiation that briefly reheated the universe.[129]
For reasons that remain uncertain, during the process of leptogenesis there was an excess in the number of electrons over positrons.[130] Hence, about one electron in every billion survived the annihilation process. This excess matched the excess of protons over anti-protons, in a condition known as baryon asymmetry, resulting in a net charge of zero for the universe.[131][132] The surviving protons and neutrons began to participate in reactions with each other—in the process known as nucleosynthesis, forming isotopes of hydrogen and helium, with trace amounts of lithium. This process peaked after about five minutes.[133] Any leftover neutrons underwent negative beta decay with a half-life of about a thousand seconds, releasing a proton and electron in the process,
For about the next 300,000–400,000 yr, the excess electrons remained too energetic to bind with atomic nuclei.[134] What followed is a period known as recombination, when neutral atoms were formed and the expanding universe became transparent to radiation.[135]
Roughly one million years after the big bang, the first generation of stars began to form.[135] Within a star, stellar nucleosynthesis results in the production of positrons from the fusion of atomic nuclei. These antimatter particles immediately annihilate with electrons, releasing gamma rays. The net result is a steady reduction in the number of electrons, and a matching increase in the number of neutrons. However, the process of stellar evolution can result in the synthesis of radioactive isotopes. Selected isotopes can subsequently undergo negative beta decay, emitting an electron and antineutrino from the nucleus.[136] An example is the cobalt-60 (60Co) isotope, which decays to form nickel-60 (60
Ni).[137]
At the end of its lifetime, a star with more than about 20 solar masses can undergo gravitational collapse to form a black hole.[138] According to classical physics, these massive stellar objects exert a gravitational attraction that is strong enough to prevent anything, even electromagnetic radiation, from escaping past the Schwarzschild radius. However, it is believed that quantum mechanical effects may allow Hawking radiation to be emitted at this distance. Electrons (and positrons) are thought to be created at the event horizon of these stellar remnants.
When pairs of virtual particles (such as an electron and positron) are created in the vicinity of the event horizon, the random spatial distribution of these particles may permit one of them to appear on the exterior; this process is called quantum tunneling. The gravitational potential of the black hole can then supply the energy that transforms this virtual particle into a real particle, allowing it to radiate away into space.[139] In exchange, the other member of the pair is given negative energy, which results in a net loss of mass-energy by the black hole. The rate of Hawking radiation increases with decreasing mass, eventually causing the black hole to evaporate away until, finally, it explodes.[140]
Cosmic rays are particles traveling through space with high energies. Energy events as high as 3.0×1020 eV have been recorded.[141] When these particles collide with nucleons in the Earth‘s atmosphere, a shower of particles is generated, including pions.[142] More than half of the cosmic radiation observed from the Earth’s surface consists of muons. The particle called a muon is a lepton which is produced in the upper atmosphere by the decay of a pion.
A muon, in turn, can decay to form an electron or positron.[143]
Observation
Aurorae are mostly caused by energetic electrons precipitating into the atmosphere.[144]
Remote observation of electrons requires detection of their radiated energy. For example, in high-energy environments such as the corona of a star, free electrons form a plasma that radiates energy due to Bremsstrahlung. Electron gas can undergo plasma oscillation, which is waves caused by synchronized variations in electron density, and these produce energy emissions that can be detected by using radio telescopes.[145]
The frequency of a photon is proportional to its energy. As a bound electron transitions between different energy levels of an atom, it will absorb or emit photons at characteristic frequencies. For instance, when atoms are irradiated by a source with a broad spectrum, distinct absorption lines will appear in the spectrum of transmitted radiation. Each element or molecule displays a characteristic set of spectral lines, such as the hydrogen spectral series. Spectroscopic measurements of the strength and width of these lines allow the composition and physical properties of a substance to be determined.[146][147]
In laboratory conditions, the interactions of individual electrons can be observed by means of particle detectors, which allow measurement of specific properties such as energy, spin and charge.[105] The development of the Paul trap and Penning trap allows charged particles to be contained within a small region for long durations. This enables precise measurements of the particle properties. For example, in one instance a Penning trap was used to contain a single electron for a period of 10 months.[148] The magnetic moment of the electron was measured to a precision of eleven digits, which, in 1980, was a greater accuracy than for any other physical constant.[149]
The first video images of an electron’s energy distribution were captured by a team at Lund University in Sweden, February 2008. The scientists used extremely short flashes of light, called attosecond pulses, which allowed an electron’s motion to be observed for the first time.[150][151]
The distribution of the electrons in solid materials can be visualized by angle resolved photoemission spectroscopy (ARPES). This technique employs the photoelectric effect to measure the reciprocal space—a mathematical representation of periodic structures that is used to infer the original structure. ARPES can be used to determine the direction, speed and scattering of electrons within the material.[152]
Plasma applications
Particle beams
During a NASA wind tunnel test, a model of the Space Shuttle is targeted by a beam of electrons, simulating the effect of ionizing gases during re-entry.[153]
Electron beams are used in welding,[154] which allows energy densities up to 107 W·cm−2 across a narrow focus diameter of 0.1–1.3 mm and usually does not require a filler material. This welding technique must be performed in a vacuum, so that the electron beam does not interact with the gas prior to reaching the target, and it can be used to join conductive materials that would otherwise be considered unsuitable for welding.[155][156]
Electron beam lithography (EBL) is a method of etching semiconductors at resolutions smaller than a micron.[157] This technique is limited by high costs, slow performance, the need to operate the beam in the vacuum and the tendency of the electrons to scatter in solids. The last problem limits the resolution to about 10 nm. For this reason, EBL is primarily used for the production of small numbers of specialized integrated circuits.[158]
Electron beam processing is used to irradiate materials in order to change their physical properties or sterilize medical and food products.[159] In radiation therapy, electron beams are generated by linear accelerators for treatment of superficial tumors. Because an electron beam only penetrates to a limited depth before being absorbed, typically up to 5 cm for electron energies in the range 5–20 MeV, electron therapy is useful for treating skin lesions such as basal cell carcinomas. An electron beam can be used to supplement the treatment of areas that have been irradiated by X-rays.[160][161]
Particle accelerators use electric fields to propel electrons and their antiparticles to high energies. As these particles pass through magnetic fields, they emit synchrotron radiation. The intensity of this radiation is spin dependent, which causes polarization of the electron beam—a process known as the Sokolov–Ternov effect.[note 8] The polarized electron beams can be useful for various experiments. Synchrotron radiation can also be used for cooling the electron beams, which reduces the momentum spread of the particles. Once the particles have accelerated to the required energies, separate electron and positron beams are brought into collision. The resulting energy emissions are observed with particle detectors and are studied in particle physics.[162]
Imaging
Low-energy electron diffraction (LEED) is a method of bombarding a crystalline material with a collimated beam of electrons, then observing the resulting diffraction patterns to determine the structure of the material. The required energy of the electrons is typically in the range 20–200 eV.[163] The reflection high energy electron diffraction (RHEED) technique uses the reflection of a beam of electrons fired at various low angles to characterize the surface of crystalline materials. The beam energy is typically in the range 8–20 keV and the angle of incidence is 1–4°.[164][165]
The electron microscope directs a focused beam of electrons at a specimen. As the beam interacts with the material, some electrons change their properties, such as movement direction, angle, relative phase and energy. By recording these changes in the electron beam, microscopists can produce atomically resolved image of the material.[166] In blue light, conventional optical microscopes have a diffraction-limited resolution of about 200 nm.[167] By comparison, electron microscopes are limited by the de Broglie wavelength of the electron. This wavelength, for example, is equal to 0.0037 nm for electrons accelerated across a 100,000-volt potential.[168] The Transmission Electron Aberration-corrected Microscope is capable of sub-0.05 nm resolution, which is more than enough to resolve individual atoms.[169] This capability makes the electron microscope a useful laboratory instrument for high resolution imaging. However, electron microscopes are expensive instruments that are costly to maintain.
There are two main types of electron microscopes: transmission and scanning. Transmission electron microscopes function in a manner similar to overhead projector, with a beam of electrons passing through a slice of material then being projected by lenses on a photographic slide or a charge-coupled device. In scanning electron microscopes, the image is produced by rastering a finely focused electron beam, as in a TV set, across the studied sample. The magnifications range from 100× to 1,000,000× or higher for both microscope types. The scanning tunneling microscope uses quantum tunneling of electrons from a sharp metal tip into the studied material and can produce atomically resolved images of its surface.[170][171][172]
Other
In the free electron laser (FEL), a relativistic electron beam is passed through a pair of undulators containing arrays of dipole magnets, whose fields are oriented in alternating directions. The electrons emit synchrotron radiation, which, in turn, coherently interacts with the same electrons. This leads to the strong amplification of the radiation field at the resonance frequency. FEL can emit a coherent high-brilliance electromagnetic radiation with a wide range of frequencies, from microwaves to soft X-rays. These devices can be used in the future for manufacturing, communication and various medical applications, such as soft tissue surgery.[173]
Electrons are at the heart of cathode ray tubes, which are used extensively as display devices in laboratory instruments, computer monitors and television sets.[174] In a photomultiplier tube, every photon striking the photocathode initiates an avalanche of electrons that produces a detectable current pulse.[175] Vacuum tubes use the flow of electrons to manipulate electrical signals, and they played a critical role in the development of electronics technology. However, they have been largely supplanted by solid-state devices such as the transistor.[176]
See also
Notes
- ^ The fractional version’s denominator is the inverse of the decimal value (along with its relative standard uncertainty of 4.2×10−13 u).
- ^ The electron’s charge is the negative of elementary charge, which has a positive value for the proton.
- ^This magnitude is obtained from the spin quantum number as
for quantum number s = 1⁄2.
See: Gupta, M.C. (2001). Atomic and Molecular Spectroscopy. New Age Publishers. p. 81. ISBN 81-224-1300-5. http://books.google.com/?id=0tIA1M6DiQIC&pg=PA81.
- ^Bohr magneton:
- ^ The classical electron radius is derived as follows. Assume that the electron’s charge is spread uniformly throughout a spherical volume. Since one part of the sphere would repel the other parts, the sphere contains electrostatic potential energy. This energy is assumed to equal the electron’s rest energy, defined by special relativity (E = mc2).
From electrostatics theory, the potential energy of a sphere with radius r and charge e is given by:where ε0 is the vacuum permittivity. For an electron with rest mass m0, the rest energy is equal to:
where c is the speed of light in a vacuum. Setting them equal and solving for r gives the classical electron radius.
See: Haken, H.; Wolf, H.C.; Brewer, W.D. (2005). The Physics of Atoms and Quanta: Introduction to Experiments and Theory. Springer. p. 70. ISBN 3-540-67274-5. http://books.google.com/?id=SPrAMy8glocC&pg=PA70.
- ^ Radiation from non-relativistic electrons is sometimes termed cyclotron radiation.
- ^ The change in wavelength, Δλ, depends on the angle of the recoil, θ, as follows,
where c is the speed of light in a vacuum and me is the electron mass. See Zombeck (2007: 393, 396).
- ^ The polarization of an electron beam means that the spins of all electrons point into one direction. In other words, the projections of the spins of all electrons onto their momentum vector have the same sign.
References
- ^ Dahl, P.F. (1997). Flash of the Cathode Rays: A History of J J Thomson’s Electron. CRC Press. p. 72. ISBN 0-7503-0453-7. http://books.google.com/?id=xUzaWGocMdMC&printsec=frontcover.
- ^ a b c Eichten, E.J.; Peskin, M.E.; Peskin, M. (1983). “New Tests for Quark and Lepton Substructure”. Physical Review Letters 50 (11): 811–814. Bibcode 1983PhRvL..50..811E. doi:10.1103/PhysRevLett.50.811.
- ^ a b Farrar, W.V. (1969). “Richard Laming and the Coal-Gas Industry, with His Views on the Structure of Matter”. Annals of Science 25: 243–254. doi:10.1080/00033796900200141.
- ^ a b c Arabatzis, T. (2006). Representing Electrons: A Biographical Approach to Theoretical Entities. University of Chicago Press. pp. 70–74. ISBN 0-226-02421-0. http://books.google.com/?id=rZHT-chpLmAC&pg=PA70.
- ^ Buchwald, J.Z.; Warwick, A. (2001). Histories of the Electron: The Birth of Microphysics. MIT Press. pp. 195–203. ISBN 0-262-52424-4. http://books.google.com/?id=1yqqhlIdCOoC&pg=PA195.
- ^ a b c d e f Thomson, J.J. (1897). “Cathode Rays”. Philosophical Magazine 44: 293. http://web.lemoyne.edu/~GIUNTA/thomson1897.html.
- ^ a b c d e P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), “The 2010 CODATA Recommended Values of the Fundamental Physical Constants” (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants [Thursday, 02-Jun-2011 21:00:12 EDT]. National Institute of Standards and Technology, Gaithersburg, MD 20899.
- ^ a b “CODATA value: proton-electron mass ratio”. National Institute of Standards and Technology. http://physics.nist.gov/cgi-bin/cuu/Value?mpsme. Retrieved 2009-07-18.
- ^ a b c d Curtis, L.J. (2003). Atomic Structure and Lifetimes: A Conceptual Approach. Cambridge University Press. p. 74. ISBN 0-521-53635-9. http://books.google.com/?id=KmwCsuvxClAC&pg=PA74.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 0-691-13512-6. http://books.google.com/?id=rDEvQZhpltEC&pg=PA236.
- ^ a b c Dahl (1997:122–185).
- ^ a b Wilson, R. (1997). Astronomy Through the Ages: The Story of the Human Attempt to Understand the Universe. CRC Press. p. 138. ISBN 0-7484-0748-0. http://books.google.com/?id=AoiJ3hA8bQ8C&pg=PA138.
- ^ a b Pauling, L.C. (1960). The Nature of the Chemical Bond and the Structure of Molecules and Crystals: an introduction to modern structural chemistry (3rd ed.). Cornell University Press. pp. 4–10. ISBN 0-8014-0333-2. http://books.google.com/?id=L-1K9HmKmUUC.
- ^ Shipley, J.T. (1945). Dictionary of Word Origins. The Philosophical Library. p. 133. ISBN 0-88029-751-4.
- ^ Baigrie, B. (2006). Electricity and Magnetism: A Historical Perspective. Greenwood Press. pp. 7–8. ISBN 0-313-33358-0. http://books.google.com/?id=3XEc5xkWxi4C&pg=PA7.
- ^ Keithley, J.F. (1999). The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s. IEEE Press. ISBN 0-7803-1193-0. http://books.google.com/?id=uwgNAtqSHuQC&pg=PA207.
- ^ “Benjamin Franklin (1706–1790)”. Eric Weisstein’s World of Biography. Wolfram Research. http://scienceworld.wolfram.com/biography/FranklinBenjamin.html. Retrieved 2010-12-16.
- ^ Myers, R.L. (2006). The Basics of Physics. Greenwood Publishing Group. p. 242. ISBN 0-313-32857-9. http://books.google.com/books?id=KnynjL44pI4C&pg=PA242.
- ^ Barrow, J.D. (1983). “Natural Units Before Planck”. Quarterly Journal of the Royal Astronomical Society 24: 24–26. Bibcode 1983QJRAS..24…24B.
- ^ Stoney, G.J. (1894). “Of the “Electron,” or Atom of Electricity”. Philosophical Magazine 38 (5): 418–420.
- ^ Soukhanov, A.H. ed. (1986). Word Mysteries & Histories. Houghton Mifflin Company. p. 73. ISBN 0-395-40265-4.
- ^ Guralnik, D.B. ed. (1970). Webster’s New World Dictionary. Prentice-Hall. p. 450.
- ^ Born, M.; Blin-Stoyle, R.J.; Radcliffe, J.M. (1989). Atomic Physics. Courier Dover. p. 26. ISBN 0-486-65984-4. http://books.google.com/?id=NmM-KujxMtoC&pg=PA26.
- ^ Dahl (1997:55–58).
- ^ DeKosky, R.K. (1983). “William Crookes and the quest for absolute vacuum in the 1870s”. Annals of Science 40 (1): 1–18. doi:10.1080/00033798300200101.
- ^ a b c Leicester, H.M. (1971). The Historical Background of Chemistry. Courier Dover Publications. pp. 221–222. ISBN 0-486-61053-5. http://books.google.com/?id=aJZVQnqcwv4C&pg=PA221.
- ^ Dahl (1997:64–78).
- ^ Zeeman, P. (1907). “Sir William Crookes, F.R.S.”. Nature 77 (1984): 1–3. Bibcode 1907Natur..77….1C. doi:10.1038/077001a0. http://books.google.com/?id=UtYRAAAAYAAJ.
- ^ Dahl (1997:99).
- ^ Thomson, J.J. (1906). “Nobel Lecture: Carriers of Negative Electricity”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1906/thomson-lecture.pdf. Retrieved 2008-08-25.
- ^ Trenn, T.J. (1976). “Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays”. Isis 67 (1): 61–75. doi:10.1086/351545. JSTOR 231134.
- ^ Becquerel, H. (1900). “Déviation du Rayonnement du Radium dans un Champ Électrique”. Comptes Rendus de l’Académie des Sciences 130: 809–815. (French)
- ^ Buchwald and Warwick (2001:90–91).
- ^ Myers, W.G. (1976). “Becquerel’s Discovery of Radioactivity in 1896”. Journal of Nuclear Medicine 17 (7): 579–582. PMID 775027. http://jnm.snmjournals.org/cgi/content/abstract/17/7/579.
- ^ Kikoin, I.K.; Sominskiĭ, I.S. (1961). “Abram Fedorovich Ioffe (on his eightieth birthday)”. Soviet Physics Uspekhi 3: 798–809. Bibcode 1961SvPhU…3..798K. doi:10.1070/PU1961v003n05ABEH005812. Original publication in Russian: Кикоин, И.К.; Соминский, М.С. (1960). “Академик А.Ф. Иоффе”. Успехи Физических Наук 72 (10): 303–321. http://ufn.ru/ufn60/ufn60_10/Russian/r6010e.pdf.
- ^ Millikan, R.A. (1911). “The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes’ Law”. Physical Review 32 (2): 349–397. Bibcode 1911PhRvI..32..349M. doi:10.1103/PhysRevSeriesI.32.349.
- ^ Das Gupta, N.N.; Ghosh, S.K. (1999). “A Report on the Wilson Cloud Chamber and Its Applications in Physics”. Reviews of Modern Physics 18: 225–290. Bibcode 1946RvMP…18..225G. doi:10.1103/RevModPhys.18.225.
- ^ a b c Smirnov, B.M. (2003). Physics of Atoms and Ions. Springer. pp. 14–21. ISBN 0-387-95550-X. http://books.google.com/?id=I1O8WYOcUscC&pg=PA14.
- ^ Bohr, N. (1922). “Nobel Lecture: The Structure of the Atom”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1922/bohr-lecture.pdf. Retrieved 2008-12-03.
- ^ Lewis, G.N. (1916). “The Atom and the Molecule”. Journal of the American Chemical Society 38 (4): 762–786. doi:10.1021/ja02261a002.
- ^ a b Arabatzis, T.; Gavroglu, K. (1997). “The chemists’ electron”. European Journal of Physics 18: 150–163. Bibcode 1997EJPh…18..150A. doi:10.1088/0143-0807/18/3/005.
- ^ Langmuir, I. (1919). “The Arrangement of Electrons in Atoms and Molecules”. Journal of the American Chemical Society 41 (6): 868–934. doi:10.1021/ja02227a002.
- ^ Scerri, E.R. (2007). The Periodic Table. Oxford University Press. pp. 205–226. ISBN 0-19-530573-6. http://books.google.com/?id=SNRdGWCGt1UC&pg=PA205.
- ^ Massimi, M. (2005). Pauli’s Exclusion Principle, The Origin and Validation of a Scientific Principle. Cambridge University Press. pp. 7–8. ISBN 0-521-83911-4. http://books.google.com/?id=YS91Gsbd13cC&pg=PA7.
- ^ Uhlenbeck, G.E.; Goudsmith, S. (1925). “Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons”. Die Naturwissenschaften 13 (47). Bibcode 1925NW…..13..953E. doi:10.1007/BF01558878. (German)
- ^ Pauli, W. (1923). “Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes”. Zeitschrift für Physik 16 (1): 155–164. Bibcode 1923ZPhy…16..155P. doi:10.1007/BF01327386. (German)
- ^ a b de Broglie, L. (1929). “Nobel Lecture: The Wave Nature of the Electron”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1929/broglie-lecture.pdf. Retrieved 2008-08-30.
- ^ Falkenburg, B. (2007). Particle Metaphysics: A Critical Account of Subatomic Reality. Springer. p. 85. ISBN 3-540-33731-8. http://books.google.com/?id=EbOz5I9RNrYC&pg=PA85.
- ^ Davisson, C. (1937). “Nobel Lecture: The Discovery of Electron Waves”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1937/davisson-lecture.pdf. Retrieved 2008-08-30.
- ^ Schrödinger, E. (1926). “Quantisierung als Eigenwertproblem”. Annalen der Physik 385 (13): 437–490. Bibcode 1926AnP…385..437S. doi:10.1002/andp.19263851302. (German)
- ^ Rigden, J.S. (2003). Hydrogen. Harvard University Press. pp. 59–86. ISBN 0-674-01252-6. http://books.google.com/?id=FhFxn_lUvz0C&pg=PT66.
- ^ Reed, B.C. (2007). Quantum Mechanics. Jones & Bartlett Publishers. pp. 275–350. ISBN 0-7637-4451-4. http://books.google.com/?id=4sluccbpwjsC&pg=PA275.
- ^ Dirac, P.A.M. (1928). “The Quantum Theory of the Electron”. Proceedings of the Royal Society of London A 117 (778): 610–624. Bibcode 1928RSPSA.117..610D. doi:10.1098/rspa.1928.0023.
- ^ Dirac, P.A.M. (1933). “Nobel Lecture: Theory of Electrons and Positrons”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1933/dirac-lecture.pdf. Retrieved 2008-11-01.
- ^ Kragh, H. (2002). Quantum Generations: A History of Physics in the Twentieth Century. Princeton University Press. p. 132. ISBN 0-691-09552-3. http://books.google.com/?id=ELrFDIldlawC&pg=PA132.
- ^ Gaynor, F. (1950). Concise Encyclopedia of Atomic Energy. The Philosophical Library. p. 117.
- ^ “The Nobel Prize in Physics 1965”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1965/. Retrieved 2008-11-04.
- ^ Panofsky, W.K.H. (1997). “The Evolution of Particle Accelerators & Colliders”. Beam Line (Stanford University) 27 (1): 36–44. http://www.slac.stanford.edu/pubs/beamline/27/1/27-1-panofsky.pdf. Retrieved 2008-09-15.
- ^ Elder, F.R.; et al. (1947). “Radiation from Electrons in a Synchrotron”. Physical Review 71 (11): 829–830. Bibcode 1947PhRv…71..829E. doi:10.1103/PhysRev.71.829.5.
- ^ Hoddeson, L.; et al. (1997). The Rise of the Standard Model: Particle Physics in the 1960s and 1970s. Cambridge University Press. pp. 25–26. ISBN 0-521-57816-7. http://books.google.com/?id=klLUs2XUmOkC&pg=PA25.
- ^ Bernardini, C. (2004). “AdA: The First Electron–Positron Collider”. Physics in Perspective 6 (2): 156–183. Bibcode 2004PhP…..6..156B. doi:10.1007/s00016-003-0202-y.
- ^ “Testing the Standard Model: The LEP experiments”. CERN. 2008. http://public.web.cern.ch/PUBLIC/en/Research/LEPExp-en.html. Retrieved 2008-09-15.
- ^ “LEP reaps a final harvest”. CERN Courier 40 (10). 2000. http://cerncourier.com/cws/article/cern/28335. Retrieved 2008-11-01.
- ^ Frampton, P.H. (2000). “Quarks and Leptons Beyond the Third Generation”. Physics Reports 330: 263–348. arXiv:hep-ph/9903387. Bibcode 2000PhR…330..263F. doi:10.1016/S0370-1573(99)00095-2.
- ^ a b c Raith, W.; Mulvey, T. (2001). Constituents of Matter: Atoms, Molecules, Nuclei and Particles. CRC Press. pp. 777–781. ISBN 0-8493-1202-7.
- ^ a b c d e f g h The original source for CODATA is Mohr, P.J.; Taylor, B.N.; Newell, D.B. (2006). “CODATA recommended values of the fundamental physical constants”. Reviews of Modern Physics 80: 633–730. Bibcode 2008RvMP…80..633M. doi:10.1103/RevModPhys.80.633.
- Individual physical constants from the CODATA are available at: “The NIST Reference on Constants, Units and Uncertainty”. National Institute of Standards and Technology. http://physics.nist.gov/cuu/. Retrieved 2009-01-15.
- ^ Zombeck, M.V. (2007). Handbook of Space Astronomy and Astrophysics (3rd ed.). Cambridge University Press. p. 14. ISBN 0-521-78242-2. http://books.google.com/?id=tp_G85jm6IAC&pg=PA14.
- ^ Murphy, M.T.; et al. (2008). “Strong Limit on a Variable Proton-to-Electron Mass Ratio from Molecules in the Distant Universe”. Science 320 (5883): 1611–1613. Bibcode 2008Sci…320.1611M. doi:10.1126/science.1156352. PMID 18566280. http://www.sciencemag.org/cgi/content/abstract/320/5883/1611.
- ^ Zorn, J.C.; Chamberlain, G.E.; Hughes, V.W. (1963). “Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron”. Physical Review 129 (6): 2566–2576. Bibcode 1963PhRv..129.2566Z. doi:10.1103/PhysRev.129.2566.
- ^ a b Odom, B.; et al. (2006). “New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron”. Physical Review Letters 97 (3): 030801. Bibcode 2006PhRvL..97c0801O. doi:10.1103/PhysRevLett.97.030801. PMID 16907490.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 261–262. ISBN 0-691-13512-6. http://books.google.com/?id=rDEvQZhpltEC&pg=PA261.
- ^ Gabrielse, G.; et al. (2006). “New Determination of the Fine Structure Constant from the Electron g Value and QED”. Physical Review Letters 97: 030802(1–4). Bibcode 2006PhRvL..97c0802G. doi:10.1103/PhysRevLett.97.030802.
- ^ Dehmelt, H. (1988). “A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius”. Physica Scripta T22: 102–110. Bibcode 1988PhST…22..102D. doi:10.1088/0031-8949/1988/T22/016.
- ^ Meschede, D. (2004). Optics, light and lasers: The Practical Approach to Modern Aspects of Photonics and Laser Physics. Wiley-VCH. p. 168. ISBN 3-527-40364-7. http://books.google.com/?id=PLISLfBLcmgC&pg=PA168.
- ^ Steinberg, R.I.; et al. (1999). “Experimental test of charge conservation and the stability of the electron”. Physical Review D 61 (2): 2582–2586. Bibcode 1975PhRvD..12.2582S. doi:10.1103/PhysRevD.12.2582.
- ^ Yao, W.-M. (2006). “Review of Particle Physics”. Journal of Physics G 33 (1): 77–115. arXiv:astro-ph/0601168. Bibcode 2006JPhG…33….1Y. doi:10.1088/0954-3899/33/1/001.
- ^ a b c Munowitz, M. (2005). Knowing, The Nature of Physical Law. Oxford University Press. pp. 162–218. ISBN 0-19-516737-6. http://books.google.com/?id=IjVtDc85CYwC&pg=PA162.
- ^ Kane, G. (October 9, 2006). “Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?”. Scientific American. http://www.sciam.com/article.cfm?id=are-virtual-particles-rea&topicID=13. Retrieved 2008-09-19.
- ^ Taylor, J. (1989). “Gauge Theories in Particle Physics”. In Davies, Paul. The New Physics. Cambridge University Press. p. 464. ISBN 0-521-43831-4. http://books.google.com/?id=akb2FpZSGnMC&pg=PA464.
- ^ a b Genz, H. (2001). Nothingness: The Science of Empty Space. Da Capo Press. pp. 241–243, 245–247. ISBN 0-7382-0610-5.
- ^ Gribbin, J. (January 25, 1997). “More to electrons than meets the eye”. New Scientist. http://www.newscientist.com/article/mg15320662.300-science–more-to-electrons-than-meets-the-eye.html. Retrieved 2008-09-17.
- ^ Levine, I.; et al. (1997). “Measurement of the Electromagnetic Coupling at Large Momentum Transfer”. Physical Review Letters 78: 424–427. Bibcode 1997PhRvL..78..424L. doi:10.1103/PhysRevLett.78.424.
- ^ Murayama, H. (March 10–17, 2006). “Supersymmetry Breaking Made Easy, Viable and Generic”. Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories. La Thuile, Italy. arXiv:0709.3041.—lists a 9% mass difference for an electron that is the size of the Planck distance.
- ^ Schwinger, J. (1948). “On Quantum-Electrodynamics and the Magnetic Moment of the Electron”. Physical Review 73 (4): 416–417. Bibcode 1948PhRv…73..416S. doi:10.1103/PhysRev.73.416.
- ^ Huang, K. (2007). Fundamental Forces of Nature: The Story of Gauge Fields. World Scientific. pp. 123–125. ISBN 981-270-645-3. http://books.google.com/?id=q-CIFHpHxfEC&pg=PA123.
- ^ Foldy, L.L.; Wouthuysen, S. (1950). “On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit”. Physical Review 78: 29–36. Bibcode 1950PhRv…78…29F. doi:10.1103/PhysRev.78.29.
- ^ Sidharth, B.G. (2008). “Revisiting Zitterbewegung”. International Journal of Theoretical Physics 48: 497–506. arXiv:0806.0985. Bibcode 2009IJTP…48..497S. doi:10.1007/s10773-008-9825-8.
- ^ Elliott, R.S. (1978). “The History of Electromagnetics as Hertz Would Have Known It”. IEEE Transactions on Microwave Theory and Techniques 36 (5): 806–823. Bibcode 1988ITMTT..36..806E. doi:10.1109/22.3600. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=3600.
- ^ Munowitz (2005:140).
- ^ Crowell, B. (2000). Electricity and Magnetism. Light and Matter. pp. 129–152. ISBN 0-9704670-4-4. http://books.google.com/?id=s9QWZNfnz1oC&pg=PT129.
- ^ Munowitz (2005:160).
- ^ Mahadevan, R.; Narayan, R.; Yi, I. (1996). “Harmony in Electrons: Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field”. Astrophysical Journal 465: 327–337. arXiv:astro-ph/9601073. Bibcode 1996ApJ…465..327M. doi:10.1086/177422.
- ^ Rohrlich, F. (1999). “The Self-Force and Radiation Reaction”. American Journal of Physics 68 (12): 1109–1112. Bibcode 2000AmJPh..68.1109R. doi:10.1119/1.1286430.
- ^ Georgi, H. (1989). “Grand Unified Theories”. In Davies, Paul. The New Physics. Cambridge University Press. p. 427. ISBN 0-521-43831-4. http://books.google.com/?id=akb2FpZSGnMC&pg=PA427.
- ^ Blumenthal, G.J.; Gould, R. (1970). “Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases”. Reviews of Modern Physics 42: 237–270. Bibcode 1970RvMP…42..237B. doi:10.1103/RevModPhys.42.237.
- ^ Staff (2008). “The Nobel Prize in Physics 1927”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1927/. Retrieved 2008-09-28.
- ^ Chen, S.-Y.; Maksimchuk, A.; Umstadter, D. (1998). “Experimental observation of relativistic nonlinear Thomson scattering”. Nature 396 (6712): 653–655. arXiv:physics/9810036. Bibcode 1998Natur.396..653C. doi:10.1038/25303.
- ^ Beringer, R.; Montgomery, C.G. (1942). “The Angular Distribution of Positron Annihilation Radiation”. Physical Review 61 (5–6): 222–224. Bibcode 1942PhRv…61..222B. doi:10.1103/PhysRev.61.222.
- ^ Buffa, A. (2000). College Physics (4th ed.). Prentice Hall. p. 888. ISBN [[Special:BookSources/0130824445}|0130824445}]].
- ^ Eichler, J. (2005). “Electron–positron pair production in relativistic ion–atom collisions”. Physics Letters A 347 (1–3): 67–72. Bibcode 2005PhLA..347…67E. doi:10.1016/j.physleta.2005.06.105.
- ^ Hubbell, J.H. (2006). “Electron positron pair production by photons: A historical overview”. Radiation Physics and Chemistry 75 (6): 614–623. Bibcode 2006RaPC…75..614H. doi:10.1016/j.radphyschem.2005.10.008.
- ^ Quigg, C. (June 4–30, 2000). “The Electroweak Theory”. TASI 2000: Flavor Physics for the Millennium. Boulder, Colorado. p. 80. arXiv:hep-ph/0204104.
- ^ Mulliken, R.S. (1967). “Spectroscopy, Molecular Orbitals, and Chemical Bonding”. Science 157 (3784): 13–24. Bibcode 1967Sci…157…13M. doi:10.1126/science.157.3784.13. PMID 5338306.
- ^ Burhop, E.H.S. (1952). The Auger Effect and Other Radiationless Transitions. Cambridge University Press. pp. 2–3. ISBN 0-88275-966-3.
- ^ a b Grupen, C. (2000). “Physics of Particle Detection”. AIP Conference Proceedings 536: 3–34. arXiv:physics/9906063. doi:10.1063/1.1361756.
- ^ Jiles, D. (1998). Introduction to Magnetism and Magnetic Materials. CRC Press. pp. 280–287. ISBN 0-412-79860-3. http://books.google.com/?id=axyWXjsdorMC&pg=PA280.
- ^ Löwdin, P.O.; Erkki Brändas, E.; Kryachko, E.S. (2003). Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per- Olov Löwdin. Springer. pp. 393–394. ISBN 1-4020-1290-X. http://books.google.com/?id=8QiR8lCX_qcC&pg=PA393.
- ^ McQuarrie, D.A.; Simon, J.D. (1997). Physical Chemistry: A Molecular Approach. University Science Books. pp. 325–361. ISBN 0-935702-99-7. http://books.google.com/?id=f-bje0-DEYUC&pg=PA325.
- ^ Daudel, R.; et al. (1973). “The Electron Pair in Chemistry”. Canadian Journal of Chemistry 52: 1310–1320. doi:10.1139/v74-201. http://article.pubs.nrc-cnrc.gc.ca/ppv/RPViewDoc?issn=1480-3291&volume=52&issue=8&startPage=1310.
- ^ Rakov, V.A.; Uman, M.A. (2007). Lightning: Physics and Effects. Cambridge University Press. p. 4. ISBN 0-521-03541-4. http://books.google.com/?id=TuMa5lAa3RAC&pg=PA4.
- ^ Freeman, G.R. (1999). “Triboelectricity and some associated phenomena”. Materials science and technology 15 (12): 1454–1458.
- ^ Forward, K.M.; Lacks, D.J.; Sankaran, R.M. (2009). “Methodology for studying particle–particle triboelectrification in granular materials”. Journal of Electrostatics 67 (2–3): 178–183. doi:10.1016/j.elstat.2008.12.002.
- ^ Weinberg, S. (2003). The Discovery of Subatomic Particles. Cambridge University Press. pp. 15–16. ISBN 0-521-82351-X. http://books.google.com/?id=tDpwhp2lOKMC&pg=PA15.
- ^ Lou, L.-F. (2003). Introduction to phonons and electrons. World Scientific. pp. 162, 164. ISBN 978-981-238-461-4. http://books.google.com/?id=XMv-vfsoRF8C&pg=PA162.
- ^ Guru, B.S.; Hızıroğlu, H.R. (2004). Electromagnetic Field Theory. Cambridge University Press. pp. 138, 276. ISBN 0-521-83016-8. http://books.google.com/?id=b2f8rCngSuAC&pg=PA138.
- ^ Achuthan, M.K.; Bhat, K.N. (2007). Fundamentals of Semiconductor Devices. Tata McGraw-Hill. pp. 49–67. ISBN 0-07-061220-X. http://books.google.com/?id=REQkwBF4cVoC&pg=PA49.
- ^ a b Ziman, J.M. (2001). Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford University Press. p. 260. ISBN 0-19-850779-8. http://books.google.com/?id=UtEy63pjngsC&pg=PA260.
- ^ Main, P. (June 12, 1993). “When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise”. New Scientist 1887: 30. http://www.newscientist.com/article/mg13818774.500-when-electrons-go-with-the-flow-remove-the-obstacles-thatcreate-electrical-resistance-and-you-get-ballistic-electrons-and-a-quantumsurprise.html. Retrieved 2008-10-09.
- ^ Blackwell, G.R. (2000). The Electronic Packaging Handbook. CRC Press. pp. 6.39–6.40. ISBN 0-8493-8591-1. http://books.google.com/?id=D0PBG53PQlUC&pg=SA6-PA39.
- ^ Durrant, A. (2000). Quantum Physics of Matter: The Physical World. CRC Press. p. http://books.google.com/books?id=F0JmHRkJHiUC&pg=PA43. ISBN 0-7503-0721-8.
- ^ Staff (2008). “The Nobel Prize in Physics 1972”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1972/. Retrieved 2008-10-13.
- ^ Kadin, A.M. (2007). “Spatial Structure of the Cooper Pair”. Journal of Superconductivity and Novel Magnetism 20 (4): 285–292. arXiv:cond-mat/0510279. doi:10.1007/s10948-006-0198-z.
- ^ “Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution”. ScienceDaily. July 31, 2009. http://www.sciencedaily.com/releases/2009/07/090730141607.htm. Retrieved 2009-08-01.
- ^ Jompol, Y.; et al. (2009). “Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid”. Science 325 (5940): 597–601. Bibcode 2009Sci…325..597J. doi:10.1126/science.1171769. PMID 19644117. http://www.sciencemag.org/cgi/content/abstract/325/5940/597.
- ^ Staff (2008). “The Nobel Prize in Physics 1958, for the discovery and the interpretation of the Cherenkov effect”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1958/. Retrieved 2008-09-25.
- ^ Staff (August 26, 2008). “Special Relativity”. Stanford Linear Accelerator Center. http://www2.slac.stanford.edu/vvc/theory/relativity.html. Retrieved 2008-09-25.
- ^ Adams, S. (2000). Frontiers: Twentieth Century Physics. CRC Press. p. 215. ISBN 0-7484-0840-1. http://books.google.com/?id=yIsMaQblCisC&pg=PA215.
- ^ Lurquin, P.F. (2003). The Origins of Life and the Universe. Columbia University Press. p. 2. ISBN 0-231-12655-7.
- ^ Silk, J. (2000). The Big Bang: The Creation and Evolution of the Universe (3rd ed.). Macmillan. pp. 110–112, 134–137. ISBN 0-8050-7256-X.
- ^ Christianto, V. (2007). “Thirty Unsolved Problems in the Physics of Elementary Particles”. Progress in Physics 4: 112–114. http://www.ptep-online.com/index_files/2007/PP-11-16.PDF.
- ^ Kolb, E.W. (1980). “The Development of Baryon Asymmetry in the Early Universe”. Physics Letters B 91 (2): 217–221. Bibcode 1980PhLB…91..217K. doi:10.1016/0370-2693(80)90435-9.
- ^ Sather, E. (Spring/Summer 1996). “The Mystery of Matter Asymmetry”. Beam Line. University of Stanford. http://www.slac.stanford.edu/pubs/beamline/26/1/26-1-sather.pdf. Retrieved 2008-11-01.
- ^ Burles, S.; Nollett, K.M.; Turner, M.S. (1999). “Big-Bang Nucleosynthesis: Linking Inner Space and Outer Space”. arXiv:astro-ph/9903300 [astro-ph].
- ^ Boesgaard, A.M.; Steigman, G. (1985). “Big bang nucleosynthesis – Theories and observations”. Annual Review of Astronomy and Astrophysics 23 (2): 319–378. Bibcode 1985ARA&A..23..319B. doi:10.1146/annurev.aa.23.090185.001535.
- ^ a b Barkana, R. (2006). “The First Stars in the Universe and Cosmic Reionization”. Science 313 (5789): 931–934. arXiv:astro-ph/0608450. Bibcode 2006Sci…313..931B. doi:10.1126/science.1125644. PMID 16917052. http://www.sciencemag.org/cgi/content/full/313/5789/931.
- ^ Burbidge, E.M.; et al. (1957). “Synthesis of Elements in Stars”. Reviews of Modern Physics 29 (4): 548–647. Bibcode 1957RvMP…29..547B. doi:10.1103/RevModPhys.29.547.
- ^ Rodberg, L.S.; Weisskopf, V. (1957). “Fall of Parity: Recent Discoveries Related to Symmetry of Laws of Nature”. Science 125 (3249): 627–633. Bibcode 1957Sci…125..627R. doi:10.1126/science.125.3249.627. PMID 17810563.
- ^ Fryer, C.L. (1999). “Mass Limits For Black Hole Formation”. Astrophysical Journal 522 (1): 413–418. arXiv:astro-ph/9902315. Bibcode 1999ApJ…522..413F. doi:10.1086/307647.
- ^ Parikh, M.K.; Wilczek, F. (2000). “Hawking Radiation As Tunneling”. Physical Review Letters 85 (24): 5042–5045. arXiv:hep-th/9907001. Bibcode 2000PhRvL..85.5042P. doi:10.1103/PhysRevLett.85.5042. PMID 11102182.
- ^ Hawking, S.W. (1974). “Black hole explosions?”. Nature 248 (5443): 30–31. Bibcode 1974Natur.248…30H. doi:10.1038/248030a0.
- ^ Halzen, F.; Hooper, D. (2002). “High-energy neutrino astronomy: the cosmic ray connection”. Reports on Progress in Physics 66: 1025–1078. arXiv:astro-ph/0204527. Bibcode 2002astro.ph..4527H. doi:10.1088/0034-4885/65/7/201.
- ^ Ziegler, J.F. (1998). “Terrestrial cosmic ray intensities”. IBM Journal of Research and Development 42 (1): 117–139. doi:10.1147/rd.421.0117.
- ^ Sutton, C. (August 4, 1990). “Muons, pions and other strange particles”. New Scientist. http://www.newscientist.com/article/mg12717284.700-muons-pions-and-other-strange-particles-.html. Retrieved 2008-08-28.
- ^ Wolpert, S. (July 24, 2008). “Scientists solve 30-year-old aurora borealis mystery”. University of California. http://www.universityofcalifornia.edu/news/article/18277. Retrieved 2008-10-11.
- ^ Gurnett, D.A.; Anderson, R. (1976). “Electron Plasma Oscillations Associated with Type III Radio Bursts”. Science 194 (4270): 1159–1162. Bibcode 1976Sci…194.1159G. doi:10.1126/science.194.4270.1159. PMID 17790910.
- ^ Martin, W.C.; Wiese, W.L. (2007). “Atomic Spectroscopy: A Compendium of Basic Ideas, Notation, Data, and Formulas”. National Institute of Standards and Technology. http://physics.nist.gov/Pubs/AtSpec/. Retrieved 2007-01-08.
- ^ Fowles, G.R. (1989). Introduction to Modern Optics. Courier Dover. pp. 227–233. ISBN 0-486-65957-7. http://books.google.com/?id=SL1n9TuJ5YMC&pg=PA227.
- ^ Staff (2008). “The Nobel Prize in Physics 1989”. The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1989/illpres/. Retrieved 2008-09-24.
- ^ Ekstrom, P. (1980). “The isolated Electron”. Scientific American 243 (2): 91–101. http://tf.nist.gov/general/pdf/166.pdf. Retrieved 2008-09-24.
- ^ Mauritsson, J.. “Electron filmed for the first time ever”. Lunds Universitet. http://www.atto.fysik.lth.se/video/pressrelen.pdf. Retrieved 2008-09-17.
- ^ Mauritsson, J.; et al. (2008). “Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope”. Physical Review Letters 100: 073003. Bibcode 2008PhRvL.100g3003M. doi:10.1103/PhysRevLett.100.073003. http://www.atto.fysik.lth.se/publications/papers/MauritssonPRL2008.pdf.
- ^ Damascelli, A. (2004). “Probing the Electronic Structure of Complex Systems by ARPES”. Physica Scripta T109: 61–74. arXiv:cond-mat/0307085. Bibcode 2004PhST..109…61D. doi:10.1238/Physica.Topical.109a00061.
- ^ Staff (April 4, 1975). “Image # L-1975-02972”. Langley Research Center, NASA. http://grin.hq.nasa.gov/ABSTRACTS/GPN-2000-003012.html. Retrieved 2008-09-20.
- ^ Elmer, J. (March 3, 2008). “Standardizing the Art of Electron-Beam Welding”. Lawrence Livermore National Laboratory. https://www.llnl.gov/str/MarApr08/elmer.html. Retrieved 2008-10-16.
- ^ Schultz, H. (1993). Electron Beam Welding. Woodhead Publishing. pp. 2–3. ISBN 1-85573-050-2. http://books.google.com/?id=I0xMo28DwcIC&pg=PA2.
- ^ Benedict, G.F. (1987). Nontraditional Manufacturing Processes. Manufacturing engineering and materials processing. 19. CRC Press. p. 273. ISBN 0-8247-7352-7. http://books.google.com/?id=xdmNVSio8jUC&pg=PA273.
- ^ Ozdemir, F.S. (June 25–27, 1979). “Electron beam lithography”. Proceedings of the 16th Conference on Design automation. San Diego, CA, USA: IEEE Press. pp. 383–391. http://portal.acm.org/citation.cfm?id=800292.811744. Retrieved 2008-10-16.
- ^ Madou, M.J. (2002). Fundamentals of Microfabrication: the Science of Miniaturization (2nd ed.). CRC Press. pp. 53–54. ISBN 0-8493-0826-7. http://books.google.com/?id=9bk3gJeQKBYC&pg=PA53.
- ^ Jongen, Y.; Herer, A. (May 2–5, 1996). “Electron Beam Scanning in Industrial Applications”. APS/AAPT Joint Meeting. American Physical Society. Bibcode 1996APS..MAY.H9902J.
- ^ Beddar, A.S. (2001). “Mobile linear accelerators for intraoperative radiation therapy”. AORN Journal 74: 700. doi:10.1016/S0001-2092(06)61769-9. http://findarticles.com/p/articles/mi_m0FSL/is_/ai_81161386. Retrieved 2008-10-26.
- ^ Gazda, M.J.; Coia, L.R. (June 1, 2007). “Principles of Radiation Therapy”. Cancer Network. http://www.cancernetwork.com/cancer-management/chapter02/article/10165/1165822. Retrieved 2008-10-26.
- ^ Chao, A.W.; Tigner, M. (1999). Handbook of Accelerator Physics and Engineering. World Scientific. pp. 155, 188. ISBN 981-02-3500-3. http://books.google.com/?id=Z3J4SjftF1YC&pg=PA155.
- ^ Oura, K.; et al. (2003). Surface Science: An Introduction. Springer-Verlag. pp. 1–45. ISBN 3-540-00545-5.
- ^ Ichimiya, A.; Cohen, P.I. (2004). Reflection High-energy Electron Diffraction. Cambridge University Press. p. 1. ISBN 0-521-45373-9. http://books.google.com/?id=AUVbPerNxTcC&pg=PA1.
- ^ Heppell, T.A. (1967). “A combined low energy and reflection high energy electron diffraction apparatus”. Journal of Scientific Instruments 44: 686–688. Bibcode 1967JScI…44..686H. doi:10.1088/0950-7671/44/9/311.
- ^ McMullan, D. (1993). “Scanning Electron Microscopy: 1928–1965”. University of Cambridge. http://www-g.eng.cam.ac.uk/125/achievements/mcmullan/mcm.htm. Retrieved 2009-03-23.
- ^ Slayter, H.S. (1992). Light and electron microscopy. Cambridge University Press. p. 1. ISBN 0-521-33948-0. http://books.google.com/?id=LlePVS9oq7MC&pg=PA1.
- ^ Cember, H. (1996). Introduction to Health Physics. McGraw-Hill Professional. pp. 42–43. ISBN 0-07-105461-8. http://books.google.com/?id=obcmBZe9es4C&pg=PA42.
- ^ Erni, R.; et al. (2009). “Atomic-Resolution Imaging with a Sub-50-pm Electron Probe”. Physical Review Letters 102 (9): 096101. Bibcode 2009PhRvL.102i6101E. doi:10.1103/PhysRevLett.102.096101. PMID 19392535.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists. Jones & Bartlett Publishers. pp. 12, 197–199. ISBN 0-7637-0192-0. http://books.google.com/?id=RqSMzR-IXk0C&pg=PA12.
- ^ Flegler, S.L.; Heckman Jr., J.W.; Klomparens, K.L. (1995). Scanning and Transmission Electron Microscopy: An Introduction (Reprint ed.). Oxford University Press. pp. 43–45. ISBN 0-19-510751-9.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists (2nd ed.). Jones & Bartlett Publishers. p. 9. ISBN 0-7637-0192-0. http://books.google.com/?id=RqSMzR-IXk0C&pg=PA9.
- ^ Freund, H.P.; Antonsen, T. (1996). Principles of Free-Electron Lasers. Springer. pp. 1–30. ISBN 0-412-72540-1. http://books.google.com/?id=73w9tqTgbiIC&pg=PA1.
- ^ Kitzmiller, J.W. (1995). Television Picture Tubes and Other Cathode-Ray Tubes: Industry and Trade Summary. DIANE Publishing. pp. 3–5. ISBN 0-7881-2100-6.
- ^ Sclater, N. (1999). Electronic Technology Handbook. McGraw-Hill Professional. pp. 227–228. ISBN 0-07-058048-0.
- ^ Staff (2008). “The History of the Integrated Circuit”. The Nobel Foundation. http://nobelprize.org/educational_games/physics/integrated_circuit/history/. Retrieved 2008-10-18.
External links
| Wikisource has the text of the 1911 Encyclopædia Britannica article Electron. |
| Wikimedia Commons has media related to: Electrons |
- “The Discovery of the Electron”. American Institute of Physics, Center for History of Physics. http://www.aip.org/history/electron/.
- “Particle Data Group”. University of California. http://pdg.lbl.gov/.
- Bock, R.K.; Vasilescu, A. (1998). The Particle Detector BriefBook (14th ed.). Springer. ISBN 3-540-64120-3. http://physics.web.cern.ch/Physics/ParticleDetector/BriefBook/.
|
|||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This information originally retrieved from http://en.wikipedia.org/wiki/Electron
on Wednesday 3rd August 2011 1:35 pm EDT
Now edited and maintained by ManufacturingET.org