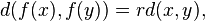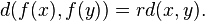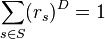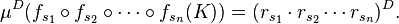Similarity

Shapes shown in the same color are similar

Two geometrical objects are called similar if they both have the same shape. More precisely, one is congruent to the result of a uniform scaling (enlarging or shrinking) of the other. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure. One can be obtained from the other by uniformly “stretching” the same amount on all directions, possibly with additional rotation and reflection, i.e., both have the same shape, or one has the same shape as the mirror image of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, nor are hyperbolas all similar to each other. If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar.

This article assumes that a scaling, enlargement or stretch can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.

1 Similar triangles
- 1.1 Angle/side similarities
2 Other similar polygons
3 Similar curves
4 Similarity in Euclidean space
5 Similarity in general metric spaces
6 Topology
7 Self-similarity
8 See also
9 External links

Similar triangles

To understand the concept of similarity of triangles, one must think of two different concepts. On the one hand there is the concept of shape and on the other hand there is the concept of scale.

In particular, similar triangles are triangles that have the same shape and are identical to one another except for scale. For a triangle, the shape is determined by its angles, so the statement that two triangles have the same shape simply means that there is a correspondence between angles that preserves their measures.

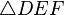Formally speaking, two triangles $\triangle ABC$ and $\triangle DEF$ are said to be similar if either of the following equivalent conditions holds:

1. Corresponding sides have lengths in the same ratio:

i.e. ${AB \over DE} = {BC \over EF} = {AC \over DF}$ . This is equivalent to saying that one triangle is an enlargement of the other.

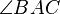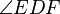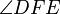2. $\angle BAC$ is equal in measure to $\angle EDF$ , and $\angle ABC$ is equal in measure to $\angle DEF$ . This also implies that $\angle ACB$ is equal in measure to $\angle DFE$ .

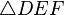When two triangles $\triangle ABC$ and $\triangle DEF$ are similar, one writes

$\triangle ABC\sim\triangle DEF \,$

The ‘is similar to’ symbol can also be expressed as three vertical lines: lll

Angle/side similarities

The following three criteria are sufficient to prove that a pair of triangles are similar. The first two state that if triangles have the same shape (AA criterion) then they are similar, and that if they are to scale (SSS criterion) then they are similar. The third criterion, SAS, combines some of the information used by each of the first two.

AA: if two triangles have two corresponding pairs of angles with the same measure then they are similar. Sometimes this criterion is also referred to as AAA because equality across triangles of two angles implies equality of the third. This criterion means that if a triangle is copied to preserve the shape, then the copy is to scale.

SSS (Three sides proportional): If the ratio of corresponding sides of two triangles does not depend on the pair of corresponding sides chosen, then the triangles are similar. This means that any triangle copied to scale is also copied in shape.

SAS (Ratio of two sides, included angle): if two sides in a triangle are proportional to two corresponding sides in another triangle, and the angles included between these sides have the same measure in each triangle, then the triangles are similar. This means that to enlarge a triangle, it is sufficient to copy one angle, and scale just the two sides that form the angle.

Other similar polygons

The concept of similarity extends to polygons with more than three sides. Given any two similar polygons, corresponding sides taken in the same sequence are proportional and corresponding angles taken in the same sequence are equal in measure. However, proportionality of corresponding sides is not by itself sufficient to prove similarity for polygons beyond triangles (otherwise, for example, all rhombi would be similar). Likewise, equality of all angles in sequence is not sufficient to guarantee similarity (otherwise all rectangles would be similar).

Similar curves

Several other types curves are similar, with all examples of that type being similar to each other. These include:

Parabola
Catenary
Graphs of the logarithm function for different bases
Logarithmic spiral

Similarity in Euclidean space

One of the meanings of the terms similarity and similarity transformation (also called dilation) of a Euclidean space is a function f from the space into itself that multiplies all distances by the same positive scalar r, so that for any two points x and y we have

$d(f(x),f(y)) = r d(x,y), \,$

where “d(x,y)” is the Euclidean distance from x to y. Two sets are called similar if one is the image of the other under such a similarity.

A special case is a homothetic transformation or central similarity: it neither involves rotation nor taking the mirror image. A similarity is a composition of a homothety and an isometry. Therefore, in general Euclidean spaces every similarity is an affine transformation, because the Euclidean group E(n) is a subgroup of the affine group.

Viewing the complex plane as a 2-dimensional space over the reals, the 2D similarity transformations expressed in terms of the complex plane are $f (z) = a z + b$ and 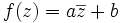$f(z)=a\overline z+b$ , and all affine transformations are of the form $f(z)=az+b\overline z+c$ (a, b, and c complex).

Similarity in general metric spaces

Sierpinski triangle. A space having self-similarity dimension ln 3 / ln 2 = log₂3, which is approximately 1.58. (from Hausdorff dimension.)

In a general metric space (X, d), an exact similitude is a function f from the metric space X into itself that multiplies all distances by the same positive scalar r, called f’s contraction factor, so that for any two points x and y we have

$d(f(x),f(y)) = r d(x,y).\, \,$

Weaker versions of similarity would for instance have f be a bi-Lipschitz function and the scalar r a limit

$\lim \frac{d(f(x),f(y))}{d(x,y)} = r.$

This weaker version applies when the metric is an effective resistance on a topologically self-similar set.

A self-similar subset of a metric space (X, d) is a set K for which there exists a finite set of similitudes $\{ f_s \}_{s\in S}$ with contraction factors $0\leq r_s < 1$ such that K is the unique compact subset of X for which

$\bigcup_{s\in S} f_s(K)=K. \,$

These self-similar sets have a self-similar measure $Î¼ D$ with dimension D given by the formula

$\sum_{s\in S} (r_s)^D=1 \,$

which is often (but not always) equal to the set’s Hausdorff dimension and packing dimension. If the overlaps between the $f s (K)$ are “small”, we have the following simple formula for the measure:

$\mu^D(f_{s_1}\circ f_{s_2} \circ \cdots \circ f_{s_n}(K))=(r_{s_1}\cdot r_{s_2}\cdots r_{s_n})^D.\,$

Topology

In topology, a metric space can be constructed by defining a similarity instead of a distance. The similarity is a function such that its value is greater when two points are closer (contrary to the distance, which is a measure of dissimilarity: the closer the points, the lesser the distance).

The definition of the similarity can vary among authors, depending on which properties are desired. The basic common properties are

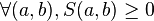
Positive defined: $\forall (a,b), S(a,b)\geq 0$
Majored by the similarity of one element on itself (auto-similarity): $S (a,b) \leq S (a,a)$ and $\forall (a,b), S (a,b) = S (a,a) \Leftrightarrow a=b$

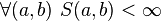More properties can be invoked, such as reflectivity ( $\forall (a,b)\ S (a,b) = S (b,a)$ ) or finiteness ( $\forall (a,b)\ S(a,b) < \infty$ ). The upper value is often set at 1 (creating a possibility for a probabilistic interpretation of the similitude).

Self-similarity

Self-similarity means that a pattern is non-trivially similar to itself, e.g., the set {.., 0.5, 0.75, 1, 1.5, 2, 3, 4, 6, 8, 12, ..}. When this set is plotted on a logarithmic scale it has translational symmetry.

External links

Animated demonstration of similar triangles

This information originally retrieved from http://en.wikipedia.org/wiki/Similarity_(geometry)
on Wednesday 27th July 2011 8:06 pm EDT
Now edited and maintained by ManufacturingET.org

Printer Friendly

Contents