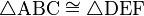Congruence

In geometry, two figures are congruent if they have the same shape and size. More formally, two sets of points are called congruent if, and only if, one can be transformed into the other by an isometry, i.e., a combination of translations, rotations and reflections.

The related concept of similarity permits a change in size.

Contents 1 Definition of congruence in analytic geometry 2 Congruence of triangles 2.1 Determining congruence 2.1.1 Side-Side-Angle 2.1.2 Angle-Angle-Angle 3 See also 4 References 5 External links

Definition of congruence in analytic geometry

In a Euclidean system, congruence is fundamental; it is the counterpart of equality for numbers. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.

A more formal definition: two subsets A and B of Euclidean space Rⁿ are called congruent if there exists an isometry f : Rⁿ → Rⁿ (an element of the Euclidean group E(n)) with f(A) = B. Congruence is an equivalence relation.

Congruence of triangles

See also Solution of triangles.

Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.

If triangle ABC is congruent to triangle DEF, the relationship can be written mathematically as:

In many cases it is sufficient to establish the equality of three corresponding parts and use one of the following results to deduce the congruence of the two triangles.

Determining congruence

Sufficient evidence for congruence between two triangles in Euclidean space can be shown through the following comparisons:

• SAS (Side-Angle-Side): If two pairs of sides of two triangles are equal in length, and the included angles are equal in measurement, then the triangles are congruent.
• SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent.
• ASA(Angle-Side-Angle): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, then the triangles are congruent.The ASA Postulate was contributed by Thales of Miletus (Greek). In most systems of axioms, the three criteria—SAS, SSS and ASA—are established as theorems. In the School Mathematics Study Group system SAS is taken as one (#15) of 22 postulates.
• AAS (Angle-Angle-Side): If two pairs of angles of two triangles are equal in measurement, and a pair of corresponding non-included sides are equal in length, then the triangles are congruent. (In British usage, ASA and AAS are usually combined into a single condition AAcorrS – any two angles and a corresponding side.)^[1]
• RHS (Right-angle-Hypotenuse-Side): If two right-angled triangles have their hypotenuses equal in length, and a pair of shorter sides are equal in length, then the triangles are congruent.

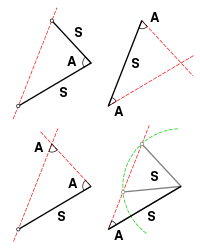
Side-Side-Angle

The SSA condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as ASS, or Angle-Side-Side) does not by itself prove congruence. In order to show congruence, additional information is required such as the measure of the corresponding angles and in some cases the lengths of the two pairs of corresponding sides. There are four possible cases:

If two triangles satisfy the SSA condition and the corresponding angles are either obtuse or right, then the two triangles are congruent. In this situation, the length of the side opposite the angle will be greater than the length of the adjacent side. Where the angle is a right angle, also known as the Hypotenuse-Leg (HL) postulate or the Right-angle-Hypotenuse-Side (RHS) condition, the third side can be calculated using the Pythagoras’ Theorem thus allowing the SSS postulate to be applied.

If two triangles satisfy the SSA condition and the corresponding angles are acute and length of the side opposite the angle is greater than or equal to the length of the adjacent side, then the two triangles are congruent.

If two triangles satisfy the SSA condition and the corresponding angles are acute and length of the side opposite the angle is equal to the length of the adjacent side multiplied by the sine of the angle, then the two triangles are congruent.

If two triangles satisfy the SSA condition and the corresponding angles are acute and length of the side opposite the angle is greater than the length of the adjacent side multiplied by the sine of the angle (but less than the length of the adjacent side), then the two triangles cannot be shown to be congruent. This is the ambiguous case and two different triangles can be formed from the given information.

Angle-Angle-Angle

In Euclidean geometry, AAA (Angle-Angle-Angle) (or just AA, since in Euclidean geometry the angles of a triangle add up to 180°) does not provide information regarding the size of the two triangles and hence proves only similarity and not congruence in Euclidean space.

However, in spherical geometry and hyperbolic geometry (where the sum of the angles of a triangle varies with size) AAA is sufficient for congruence on a given curvature of surface.^[2]

See also

• Euclidean plane isometry
• CPCTC

References

External links

Wikimedia Commons has media related to: Congruence

• The SSS at Cut-the-Knot
• The SSA at Cut-the-Knot
• Interactive animations demonstrating Congruent angles, Congruent line segments, Congruent triangles, Congruent polygons