Orthographic Projection
When you are called upon to draw a three-dimensional object or figure, it is customary to represent the parts and forms on the
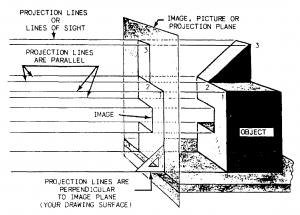
flat plane of the drafting paper in such a manner that all features are shown in their true dimensions and in their true relationship with other features on that part of the object. To do this, you must draw a number of views of the object from different angles. Projecting these essential views into a single plane is known as ORTHOGRAPHIC PROJECTION.
The term orthographic is derived from the word orthos meaning perpendicular or right-angular.
Origin
The orthographic projection has been known since antiquity, with its cartographic uses being well documented. Hipparchus used the projection in the 2nd century B.C. to determine the places of star-rise and star-set. In about 14 B.C., Roman engineer Marcus Vitruvius Pollio used the projection to construct sundials and to compute sun positions.[2]
Vitruvius also seems to have devised the term orthographic (from the Greek orthos (= “straight”) and graphē (= “drawing”) for the projection. However, the name analemma, which also meant a sundial showing latitude and longitude, was the common name until François d’Aguilon of Antwerp promoted its present name in 1613.[2]
The earliest surviving maps on the projection appear as woodcut drawings of terrestrial globes of 1509 (anonymous), 1533 and 1551 (Johannes Schöner), and 1524 and 1551 (Apian).[2]
Multiview orthographic projections
With multiview orthographic projections, up to six pictures of an object are produced, with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of two schemes: first-angle or third-angle projection. In each, the appearances of views may be thought of as being projected onto planes that form a 6-sided box around the object. Although 6 different sides can be drawn 3 sides of a drawing give enough information to make a 3D object. These views are known as front view, top view and right side view.
Pictorials
Within orthographic projection there is the subcategory known as pictorials. Axonometric pictorials show an image of an object as viewed from a skew direction in order to reveal all three directions (axes) of space in a single picture.[3] Orthographic pictorial instrument drawings are often used to approximate graphical perspective projections, but there is attendant distortion in the approximation. Because pictorial projections inherently have this distortion, in the instrument drawing of pictorials, great liberties may then be taken for economy of effort and best effect. Orthographic pictorials rely on the technique of axonometric projection (“to measure along axes”).
See also
|
References
- ^ a b Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. pp. 22. ISBN 0801472806. http://books.google.com/?id=4Y_YqOlXoxMC&pg=PA22&lpg=PA22&dq=axonometric+orthographic&q=axonometric%20orthographic.
- ^ a b c Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections pp. 16–18. Chicago and London: The University of Chicago Press. ISBN 0-226-76746-9.
- ^ Mitchell, William; Malcolm McCullough (1994). Digital design media. John Wiley and Sons. pp. 169. ISBN 0471286664. http://books.google.com/?id=JrZoGgQEhKkC&pg=PA169&dq=axonometric+orthographic#v=onepage&q=axonometric%20orthographic.
External links
|
||||||||||||||
| This geometry-related article is a stub. You can help Wikipedia by expanding it. |
This information originally retrieved from http://en.wikipedia.org/wiki/Orthographic_projection
on Thursday 28th July 2011 12:26 pm EDT
Now edited and maintained by ManufacturingET.org
