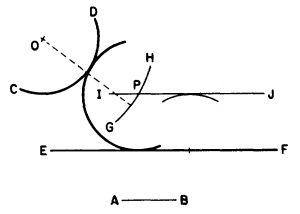
The problem in figure 4-35 is to draw a circular arc with a radius equal to AB, tangent to the circular arc CD and to the straight line EF. Set a compass to a radius equal to the radius of the circular arc CD plus the given radius AB (which is indicated by the dashed line shown), and, with O as a center, strike the arc GH. Draw a line IJ parallel to EF at a distance from EF equal to AB. The point of intersection (P) between GH and IJ is the center of the circle of which an arc of the given radius is tangent to CD and EF.
