Regular Hexagon in a Given Circumscribed Circle
Many bolt heads and nuts are hexagonal (six-sided) in shape. Figure 4-26 shows a method of constructing a regular hexagon in a given circumscribed circle. The diameter of the circumscribed circle has the same length as the long diameter of the hexagon. The radius of the circumscribed circle (which equals one-half the long diameter of the hexagon) is equal in length to the length of a side. Lay off the horizontal diameter AB and vertical diameter CD. OB is the radius of the circle. From C, draw a line CE equal to OB; then lay off this interval around the circle, and connect the points of intersection.
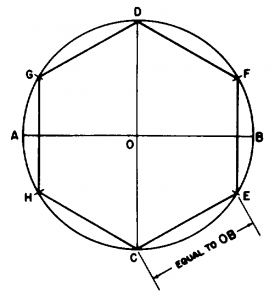Fig. 4-26 Construction of a Regular Hexagon
Triangle Method
Figure 4-27 shows another method of constructing a regular hexagon in a given circumscribed circle. Draw vertical diameter AB, and use a T square and a 30°/60° triangle to draw BC from B at 30° to the horizontal. Set a compass to BC, lay off this interval around the circumference, and connect the points of intersection.
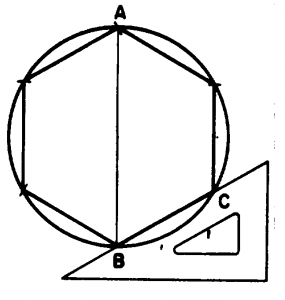Fig. 4-27 Construction of a Regular Hexagon, Circumscribed Circle, Triangle Method
Regular Hexagon on a Given Inscribed Circle
Figure 4-28 shows a method of constructing a regular hexagon on a given inscribed circle. Draw horizontal diameter AB and vertical center line. Draw lines tangent to the circle and perpendicular to AB at A and B. Use a T square and a 30°/60° triangle to draw the remaining sides of the figure tangent to the circle and at 30° to the horizontal.
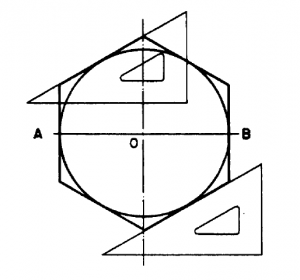Fig. 4-28 Construction of a Hexagon, Inscribed Circle, Triangle Method
(Source: NAVEDTRA 14069, U.S. Navy)
